What is the Tetrahedron Problem in H.E. Huntley's 'The Divine Proportion'?

[Dschumanji]

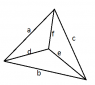
I was skimming through the book "The Divine Proportion a Study in Mathematical Beauty" by H.E. Huntley and found an interesting passage labeled "The Tetrahedron Problem." The problem is stated like this:

The faces of a tetrahedron are all scalene triangles similar to one another, but not all congruent, with integral sides. The longest side does not exceed 50. Show its network. The limitation to integral values being waived, show that the ratio of the length of the longest to that of the shortest edge has a limiting value, and find it.

This is how his solution begins:

Two triangles may have five parts of the one congruent with five parts of the other without being congruent triangles. If the triangles are not congruent, their congruent parts cannot include the three sides. Hence the triangles must be equiangular, and it is easily shown that the lengths of the sides must be in geometrical progression...

I've been scratching my head wondering what the hell this guy is trying to convey with the first two sentences (no images are provided in the text). What makes it even worse is the absence of a proof that the sides of whatever he is talking about MUST be in geomtric progression. Could anyone shed some light on this?

 

[uart]

Yeah he does a bad job of explaining it, but putting it simply he's looking at how many sides can two similar triangles have in common without being congruent.

Obviously if they're similar all then all angles are the same (equiangular) but he goes further to say that they can also have 2 equal sides if the sides are in a geometric ratio.

For example consider the two triangles with sides (1, 1.5, 2.25) and (1.5, 2.25 and 3.375). These are similar because they have all three sides in the same ratio (1:1.5) but clearly they are not congruent. Those two triangles also have 5 things in common, two sides and three angles. Clearly this is the "best" (most things in common) we can do without making the two triangles congruent.

Hope that helps.

 

[Dschumanji]

That is extremely helpful, Uart! Thank you so much!

 

[willem2]

I don't think the proof that the sides must be in a geometric procession is
all that obvious.

suppose you have a tetrahedron with edges a,b,c,d,e,f

It's always possible to rotate the tetrahedron, so a there is no larger side than a,
and then reflect it, so that b<c. b=c isn't possible, because triangle (a,b,c) is scalene.

This means that b,c,d and f are larger than a, because they are a part of a triangle that also has a as a side.

since a is the smallest side of triangle (a,b,c) as well as triangle (a,f,d) we must have

(f/a = b/a and e/a = c/a) => (f=b and e = c) or
(e/a = b/a and f/a = c/a) => (e=b and f=c)

e = b isn't possible since triang;e (b,d,e) is scalene, so the only remaining option is

f = b and d = c

If we now look at triangle (b,d,e), the ratio d/b = c/b must be equal to b/a or to c/a

c/b = c/a gives a = c which isn't possible with scalene triangles, so c/b = b/a and b^2 = ac.
b is the geometric mean of a and c. This proves a,b,c is a geometric series, with ratio: r = \sqrt {\frac {c} {a}}

b = f = ra
c = d = (r^2)a

since c>a, r>1

since d/b is equal to b/a, e/b must be equal to c/a or a/c

e/b = a/c => ec = ab => e(r^2)a = a (ra) => re = a, so e<a, but a was the smallest side.

e/b = c/a => bc = ae => (r^3)(a^2) = ae => e = a(r^3), so e is the next term of the geometric series.