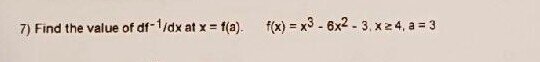SUMMARY
The discussion focuses on finding the value of the inverse derivative at \( x = f(a) \) for the function \( f(x) = x^3 - 6x^2 - 3 \) with \( a = 3 \). Participants confirm that the inverse function can be derived using implicit differentiation and the formula \( \left[f^{-1}\right]'(a) = \frac{1}{f'\left(f^{-1}(a)\right)} \). The critical steps include verifying the one-to-one nature of \( f(x) \) on the interval \([4, \infty)\) and solving for \( f^{-1}(3) \), which yields approximately \( 6.1582 \). The final calculation of the inverse derivative results in \( \left[f^{-1}\right]'(3) \approx 0.02508 \).
PREREQUISITES
- Understanding of implicit differentiation
- Familiarity with inverse functions and their derivatives
- Knowledge of polynomial functions and their properties
- Ability to solve cubic equations
NEXT STEPS
- Learn about the properties of one-to-one functions and their inverses
- Study implicit differentiation techniques in calculus
- Explore the application of the derivative of inverse functions
- Practice solving cubic equations using numerical methods or graphing tools
USEFUL FOR
Mathematics students, educators, and professionals involved in calculus, particularly those focusing on inverse functions and their applications in real-world problems.