BWV
- 1,618
- 1,969
Reading this piece with a number of proofs of the divergence of the harmonic series
http://scipp.ucsc.edu/~haber/archives/physics116A10/harmapa.pdf
and this example states: 'While not completely rigorous, this proof is thought-provoking nonetheless. It may provide a good exercise for students to find possible flaws in the argument.'
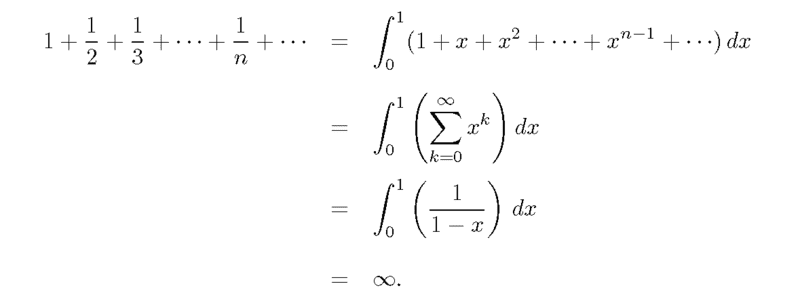
not being any good at proofs, curious what flaws or lack of rigor there is here
http://scipp.ucsc.edu/~haber/archives/physics116A10/harmapa.pdf
and this example states: 'While not completely rigorous, this proof is thought-provoking nonetheless. It may provide a good exercise for students to find possible flaws in the argument.'
not being any good at proofs, curious what flaws or lack of rigor there is here