- #1
mcastillo356
Gold Member
- 560
- 267
- TL;DR Summary
- Pseudophilosophal question about a definition
Hi, PF, I've got a quote, and a philosophical question
Figure shown suggests that a function ##f(x)## can have local extreme values only at ##x## points of three special types:
(i) Critical points of ##f## (points ##x## in ##\mathfrak{D}(f)## where ##f'(x)=0##)
(ii) Singular points of ##f## (points ##x## in ##\mathfrak{D}(f)## where ##f'(x)## is not defined)
(iii) Endpoints of the domain of ##f## (points in ##\mathfrak{D}(f)## that do not belong to any open interval contained in ##\mathfrak{D}(f)##)
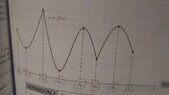
And now my "brainstorm": (iii) is not defined as "reductio ad absurdum"; not "principle of exclusion".
My question: what kind of argument makes use of? I'm just overthinking? Why does talk about closed intervals in such a "implicit" (suggested, but not communicated directly) way?
PS: I'm not sure of the LaTeX used, and insecure about "Preview" tool, so I will click "Post thread". Please check. Thanks!
Figure shown suggests that a function ##f(x)## can have local extreme values only at ##x## points of three special types:
(i) Critical points of ##f## (points ##x## in ##\mathfrak{D}(f)## where ##f'(x)=0##)
(ii) Singular points of ##f## (points ##x## in ##\mathfrak{D}(f)## where ##f'(x)## is not defined)
(iii) Endpoints of the domain of ##f## (points in ##\mathfrak{D}(f)## that do not belong to any open interval contained in ##\mathfrak{D}(f)##)

And now my "brainstorm": (iii) is not defined as "reductio ad absurdum"; not "principle of exclusion".
My question: what kind of argument makes use of? I'm just overthinking? Why does talk about closed intervals in such a "implicit" (suggested, but not communicated directly) way?
PS: I'm not sure of the LaTeX used, and insecure about "Preview" tool, so I will click "Post thread". Please check. Thanks!
 ): Why does my textbook, "Calculus", by Robert A. Adams, defines endpoints in terms of open intervals?
): Why does my textbook, "Calculus", by Robert A. Adams, defines endpoints in terms of open intervals?

