What logical error am I making? (solving for T)

[Callista]

Homework Statement

Homework Equations

Fg=mg

The Attempt at a Solution

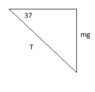
I tried to set this up as two "triangles".

&&

left triangle:
sin(37)=mg/T
T1=mg/sin(37)
T1=202.72

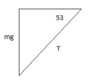
right triangle:
sin(53)=mg/T
T2=mg/sin(53)
T2=152.761

I now know the correct answers are T1=73.4N and T2=97.4. However, I'm not sure what logical fault I'm making when I originally tried to solve the problem using the above method.

Thanks for your help.

EDIT 4. Solution
My mistakes were that I needed to consider all three cables, and that T1y≠T2y.

 

[phinds]

Well, your first problem is that you are taking it as being the case that each angled rope supports the entire weight, so you are doing your calculations based on a traffic light weight of 244N

 

[Orodruin]

Hint: Force equilibrium for the connection point of the three wires.

 

[kuruman]

However, I'm not sure what logical fault I'm making when I originally tried to solve the problem using the above method.

Your triangles are OK but misinterpreted. Since the 3 forces add to zero, they should form a closed triangle when you add the vectors using the "tail-to-tip" graphic method. Specifically here the vector addition triangle you get is a 3-4-5. If you follow the hint by @Orodruin, and look at the forces acting on the connection point, you will realize that T₁ points "up and to the left", T₂ points "up and to the right" and T₃ (the weight) is vertical. Your triangles show one vertical force but they also show horizontal forces which can't be. If you rotate one of these triangles so that the hypotenuse is vertical, you will see that the right sides correctly point "up and to the left" and "up and to the right" in the vector addition diagram. In short, you have mislabeled the weight $mg$ as a right side in your triangles. Just because you drew one side vertical does not mean that it represents the weight.