What type of equation is this?

[Const@ntine]

Hi! I recently came across this pic:

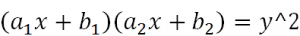
Problem is, I have no clue how to tackle this. I didn't find it in any textbooks or anything, so I don't know where to look for it. Sorry if it's a "weird" question, but it's been eating at me for a couple of hours now. I saw it categorized as "high school algebra", but I don't remember seeing this anywhere, so I'm a bit at a loss (I'm not based in the US though, so I guess there's that to take into account).

A link to a wikipedia article or something would be nice, but any help is appreciated!

 

[scottdave]

It is a Hyperbola. I picked some values for a1, b1, a2, and b2 and you can see a plot here. http://www.wolframalpha.com/input/?i=(2x+++1)(x+++3)+=+y^2

 

[fresh_42]

You might have a look on quadratic functions
https://en.wikipedia.org/wiki/Quadratic_function
and conic sections
https://en.wikipedia.org/wiki/Conic_section.

 

[fresh_42]

It is a Hyperbola. I picked some values for a1, b1, a2, and b2 and you can see a plot here. http://www.wolframalpha.com/input/?i=(2x+++1)(x+++3)+=+y^2

It can also be a parabola and and ellipse, depending on the signs of the parameters.

 

[Const@ntine]

It is a Hyperbola. I picked some values for a1, b1, a2, and b2 and you can see a plot here. http://www.wolframalpha.com/input/?i=(2x+++1)(x+++3)+=+y^2

Oh darn, yeah. It's not a "solve for x" equation, it represents a locus. Thanks!

You might have a look on quadratic functions
https://en.wikipedia.org/wiki/Quadratic_function
and conic sections
https://en.wikipedia.org/wiki/Conic_section.

It can also be a parabola and and ellipse, depending on the signs of the parameters.

Yeah, I've gone through these at HS in multiple years. I just got so hanged up on "searching for x" that I forgot about them completely. I really got to brush up on them some time...

Thanks for the help, both of you!

 

[scottdave]

It can also be a parabola and and ellipse, depending on the signs of the parameters.

Oh yeah, if a1 and a2 are opposite signs then you get an ellipse.

 

[mathwonk]

you can always look at it abstractly at first at least to get a qualitative idea. so the first observation is that it has degree 2 and is in 2 variables. so it is a conic in the x,y plane. note then that for each choice of x, there are usually two values of y, square roots of the left hand side for that x. Next recall that only non negative numbers have square roots, so there may be no values of y for some values of x, those that make the left side negative. so it seems to be some curve in the plane that projects to the x-axis so that each point on the x-axis has either zero, one, or two points over it, where there is one point iff the left hand side is zero, and none iff the left hand side is negative. thus we could have an ellipse, symmetric about the x axis, or a hyperbola. but apparently not a parabola. wait a minute, if the LHS is just x, we do get a parabola, x = y^2, and this does seem to be possible, as fresh said. ah yes, but you cannot get an ordinary vertical parabola, y=x^2.