What's the difference between 1000e^0.05t and 1000*1.05^t?

[Karagoz]

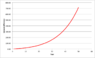
We have a population of y = 1000 at year 1980 (call it year 0).

Every year the population growth rate is 5% per year.

y' shows the growth rate of the y (population).

Since the population grows by 5% every year, the growth rate is:
y' = 0.05y.

This is a simple differential equation.
When y(0) = 1000

Then using a math software, the formula for the population is:
y(t) = 1000*e^(0.05t)

OR

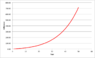
We have a population of z = 1000 at year (1980) (call it year 0)

The population growth rate 5% per year.

Since the population grows by 5% per year, we can say:
z(t) = 1000*(1+0.05)^t = 1000*1.05^t

Derivation of z(t):
z’(t) = 1000(ln1.05)*e^(t*ln1.05)

Written as differential equation:

z’(t)=(ln1.05)*z(t)

The formula similar to z(t) is used when describing the growth of a money (in a bank at a interest rate of 5%).

Both the formula y(t) and formula z(t) describes growth rate by 5% per year.

But it’s obvious that z(t) ≠ y(t)

What is the difference between y(t) = 1000*e^(0.05t) and z(t) = 1000*1.05^t when both describes a growth rate of 5% per year?

What does z(t) describe and what does y(t) describe, and what’s the difference between what each formula describe?

 

[kuruman]

What is the difference between y(t) = 1000*e^(0.05t) and z(t) = 1000*1.05^t when both describes a growth rate of 5% per year?

The difference is that y(t) is the exact description and z(t) is an approximation. If you write $y(t)=y_0e^{\lambda~t}$ and do a series expansion for the exponential, you get $y(t)=y_0 (1 +\lambda t+\lambda t^2/2+\lambda t^3/6 +...)=y_0 \sum_{k=0} ^{\infty} (\lambda t)^k/k!$
Here $y_0=1000$ and $\lambda = 0.05$. Your expression for z(t) tosses out all terms higher than first order, therefore it is approximately correct and not equal to y(t).

 

[Karagoz]

To clarify my question:
When calculating what the value of the money C will be after x years, when having an interest rate at n, we use the formula:

f(x) = C*(1+n)^x

E.g. z(t) = 1000*(1+0.05)^t = 1000*1.05^t

But why don't we use the other formula: g(x) = C*e^(0.05n)?

What would it mean if we used g(x) instead of f(x) when calculating how the value C in a bank account will after x years with an interest rate n?

 

[kuruman]

What would it mean if we used g(x) instead of f(x) when calculating how the value C in a bank account will after x years with an interest rate n?

The plot below shows the difference 1000*e^0.05*t - 1000*1.05^t for 0 < t < 50 years. At the end of 50 years, you will be able to withdraw $12182.49 according to the exponential calculation and $11467.40 according to the approximation, a shortfall of $715.09.

But why don't we use the other formula: g(x) = C*e^(0.05n)?

It's not that "we" don't use the exponential formula, it's that the banks don't use it. Any guesses why? If you choose a bank that compounds interest more often than yearly, your interest will be reinvested sooner so the bank keeps less of your money.

 

[Karagoz]

So the formula f(x) means yearly interest of n is compounded once a year.

But if banks did use g(x), that would mean the yearly interest of n is compounded far more frequently?

 

[kuruman]

But if banks did use g(x), that would mean the yearlt interest of n was compounded every second?

Or millisecond, or microsecond, or ...

Edit: Some banks compound interest quarterly, some monthly and some daily.