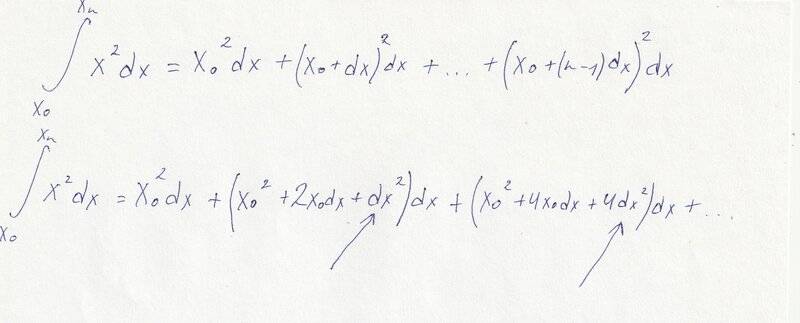Discussion Overview
The discussion revolves around the neglect of high-order terms in integral sums, particularly in the context of infinitesimal calculus and Riemann sums. Participants explore the implications of treating differentials and infinitesimals in calculus, questioning the validity of certain mathematical steps and interpretations.
Discussion Character
- Exploratory
- Debate/contested
- Mathematical reasoning
Main Points Raised
- One participant states that high-order terms can be neglected in expressions like ##f(x+dx)-f(x)##, specifically for the function ##y=x^2##, leading to ##dy=2xdx##.
- Another participant challenges the notion of ##dx## as an infinitesimal in integrals, asserting that it is merely a notation in integration and not a differential.
- A different participant expresses a lack of familiarity with infinitesimal calculus, indicating a gap in understanding the topic.
- One participant critiques the original poster's interpretation of the differential, emphasizing that the term ##dx^2## does not arise from the definition of the differential of the function.
- There is a mention of using Riemann sums to evaluate definite integrals, with a suggestion that the original source material may be outdated and not reflective of modern practices.
- Participants discuss the division of intervals in Riemann sums and the notation used, contrasting it with the use of ##dx## in older texts.
Areas of Agreement / Disagreement
Participants express differing views on the treatment of differentials and infinitesimals, with no consensus reached regarding the validity of neglecting high-order terms in integral sums or the interpretation of ##dx##.
Contextual Notes
There are unresolved assumptions regarding the definitions of differentials and infinitesimals, as well as the applicability of older calculus texts to modern understanding. The discussion reflects varying levels of familiarity with the concepts involved.