Homework Help Overview
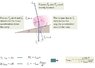
The discussion revolves around the dynamics of a uniform ball rolling down a ramp, specifically focusing on the role of friction in the motion. Participants are examining the equations governing the motion and the forces acting on the ball, including gravitational and frictional forces.
Discussion Character
- Exploratory, Conceptual clarification, Assumption checking
Approaches and Questions Raised
- Participants are questioning the derivation of specific equations related to friction and acceleration. There is an exploration of the implications of friction on the ball's ability to roll versus skid, and some participants are reflecting on the vector nature of forces involved.
Discussion Status
Some participants have provided insights into the relationship between friction and motion, while others are still seeking clarity on specific equations and concepts. There is an acknowledgment of confusion regarding the application of certain principles, and guidance has been offered to help navigate the problem.
Contextual Notes
Participants note constraints such as the original poster's reliance on visual aids for problem statements and the potential impact of exam pressures on their approach to the discussion. There is also mention of the need for clearer communication in presenting questions.