solarmidnightrose
- 28
- 10
- Homework Statement
- I've been trying to calculate the rotational inertia of this rotating gondola on this ride at this theme park.
However, they do not directly give me a specific formula to use-because with different objects, there are different formulae that you use to determine the rotational inertia of an object
mass of gondola = 6 tonne (6000kg)
radius = 3m
I will attach a picture of what it looks like
- Relevant Equations
- I have attached a picture of different possible formulae's
Picture of gondola:

Formulae:
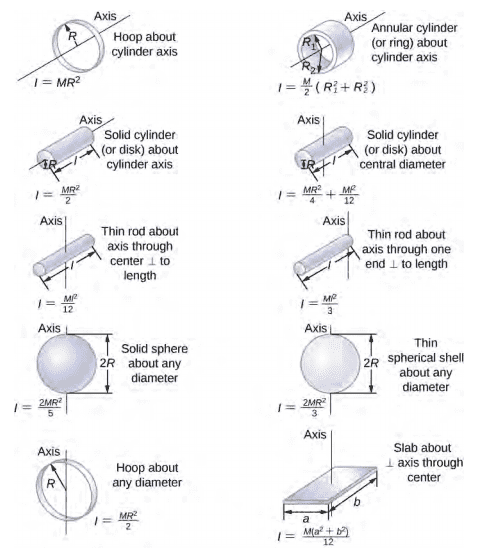
Initially, I used the equation: I=mr^2
Formulae:
Initially, I used the equation: I=mr^2
I=(6000)x(3)^2
T=54,000kgm^2
(but apparently this is incorrect)
So, basically, I don't know which formula would suit best for the gondola (the picture above). I would consider the gondola a hollow object as the mass is concentrated on the outer edges.