Which node satisfies this property?

  • Context: MHB 
  • Thread starter Thread starter evinda
  • Start date Start date
  • Tags Tags
    Property
Click For Summary

Discussion Overview

The discussion revolves around identifying the structure of a binary tree based on a given pre-order traversal and specific properties of node relationships within the tree. Participants explore how to determine the placement of nodes and whether the tree satisfies the stated conditions.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested

Main Points Raised

  • Some participants assert that the first node in the pre-order traversal, $9$, is the root of the tree.
  • There is a proposal that $17$ will be a child of $9$, but uncertainty exists regarding whether it should be a left or right child.
  • Some participants question the implications of the pre-order traversal for determining the left and right children of the root.
  • There is a suggestion that $11$ cannot be a child of $9$, leading to further inquiry about the structure of the tree.
  • Participants discuss potential tree structures that could yield the same pre-order traversal, raising questions about whether multiple valid trees exist.
  • Some participants conclude that the tree structure proposed satisfies the problem statement criteria, while others express doubt and seek clarification.
  • There is a discussion about whether the identified tree is the only possible configuration, with some participants asserting that there were no choices made during construction.

Areas of Agreement / Disagreement

Participants express differing views on the placement of nodes and the implications of the pre-order traversal. While some believe they have arrived at a satisfactory tree structure, others question whether it is the only possible configuration. The discussion remains unresolved regarding the uniqueness of the tree structure.

Contextual Notes

Participants highlight the importance of the properties of the binary tree in determining node placement, but the discussion does not resolve the implications of these properties on the overall structure.

evinda
Gold Member
MHB
Messages
3,741
Reaction score
0
Hi! (Smirk)

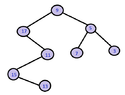
It is a given binary tree $T$, for each node $ n$ of which , all the keys of the nodes of the left subtree of $n$ are greater than the key of $n$ and all the keys of the nodes of the right subtree of $n$ are smaller than the key of $n$.

We suppose that $T$ contains the nodes $3,5,7,9,11,13,15,17$ and we are given that the pre-order traversal of the tree, gives as result the numbers in this row: $9,17,11,15,13,5,7,3$.
I have to draw the tree.

How can I find the first node $n$, which satisfies the first property? (Thinking)
 
Technology news on Phys.org
evinda said:
Hi! (Smirk)

It is a given binary tree $T$, for each node $ n$ of which , all the keys of the nodes of the left subtree of $n$ are greater than the key of $n$ and all the keys of the nodes of the right subtree of $n$ are smaller than the key of $n$.

We suppose that $T$ contains the nodes $3,5,7,9,11,13,15,17$ and we are given that the pre-order traversal of the tree, gives as result the numbers in this row: $9,17,11,15,13,5,7,3$.
I have to draw the tree.

How can I find the first node $n$, which satisfies the first property? (Thinking)

Hey! (Happy)

A pre-order visits first the root of each node, then the left subtree (beginning with its root), and then the right subtree. (Nerd)

So we can already tell that $9$ is the root of the tree.
To which subtree will $17$ belong? (Wondering)
 
I like Serena said:
Hey! (Happy)

A pre-order visits first the root of each node, then the left subtree (beginning with its root), and then the right subtree. (Nerd)

So we can already tell that $9$ is the root of the tree.
To which subtree will $17$ belong? (Wondering)

So, does this means that $17$ and $11$ will be the children of $9$?
If so, can we conclude from a pre-order which will be the left child and which the right? (Thinking)
 
evinda said:
So, does this means that $17$ and $11$ will be the children of $9$?
If so, can we conclude from a pre-order which will be the left child and which the right? (Thinking)

$17$ will definitely be a child of $9$.
What does the problem statement say about whether it should be left or right? (Wondering)

As for $11$, that comes later, but I don't think it can be a child of $9$. (Shake)
 
I like Serena said:
$17$ will definitely be a child of $9$.
What does the problem statement say about whether it should be left or right? (Wondering)
Since the keys of the nodes of the left subtree are greater than the key, does this mean that 17 is the left child of 9?

I like Serena said:
As for $11$, that comes later, but I don't think it can be a child of $9$. (Shake)

How can we find then the right child of 9? :confused:

What do we conclude then from the fact that 11 is at the third position of the pre-order? (Thinking)
 
evinda said:
Since the keys of the nodes of the left subtree are greater than the key, does this mean that 17 is the left child of 9?

Yes. (Nod)
How can we find then the right child of 9? :confused:

What do we conclude then from the fact that 11 is at the third position of the pre-order? (Thinking)

Suppose we look at the tree:
Code: 
    9
  /   \
17     11
What is then its pre-order? (Wondering)
Does the tree satisfy the problem statement criteria?

Can you think of another tree that has the same pre-order? (Wondering)
 
I like Serena said:
Suppose we look at the tree:
Code: 
    9
  /   \
17     11
What is then its pre-order? (Wondering)

It is 9,17,11, right? (Thinking)

I like Serena said:
Does the tree satisfy the problem statement criteria?
Yes, the problem statement criteria are satisfied.. (Nod) Or am I wrong? (Thinking)

I like Serena said:
Can you think of another tree that has the same pre-order? (Wondering)

Isn't this the only one? (Thinking)
 
evinda said:
It is 9,17,11, right? (Thinking)

Yep! (Nod)
evinda said:
and all the keys of the nodes of the right subtree of $n$ are smaller than the key of $n$.
Yes, the problem statement criteria are satisfied.. (Nod) Or am I wrong? (Thinking)

Since $11$ is in the right sub tree of $9$, is it smaller? (Wondering)
Isn't this the only one? (Thinking)

How about:
Code: 
     9
    /
  17
 /
11

Or:
Code: 
     9
    /
  17
    \
    11
(Wondering)
 
I like Serena said:
Since $11$ is in the right sub tree of $9$, is it smaller? (Wondering)

Oh no! I am sorry! (Blush)

I like Serena said:
How about:
Code: 
     9
    /
  17
 /
11

Or:
Code: 
     9
    /
  17
    \
    11
(Wondering)

Oh yes, you are right! (Tmi)
 
  • #10
So, the first number of the pre-order is always the root, right? (Thinking)
Then, do we know that the next two numbers are the children of the root?
Or do we know this only for the second one? Or for none of them? (Thinking)
 
  • #11
evinda said:
Oh yes, you are right! (Tmi)

Which of these satisfies the criteria of the problem statement? (Wondering)
 
  • #12
I like Serena said:
Which of these satisfies the criteria of the problem statement? (Wondering)

This:

Code: 
     9
    /
  17
    \
    11

satisfies the criteria of the problem statement, right? (Thinking)
 
  • #13
evinda said:
This:

Code: 
     9
    /
  17
    \
    11

satisfies the criteria of the problem statement, right? (Thinking)

Yep! (Nod)
 
  • #14
I like Serena said:
Yep! (Nod)

Nice! And 15 will be now the left child of 11? Or am I wrong? (Thinking)
 
  • #15

Attachments

  • tree7.png
    tree7.png
    3.1 KB · Views: 118
  • #16
evinda said:
So, will the tree be like that?

Yep! (Party)
 
  • #17
I like Serena said:
Yep! (Party)

Great! (Party) And this is the only tree, that can be found, right? (Thinking)
 
  • #18
evinda said:
Great! (Party) And this is the only tree, that can be found, right? (Thinking)

When you were building up the tree, did you have any choices to make? (Wondering)
 
  • #19
I like Serena said:
When you were building up the tree, did you have any choices to make? (Wondering)

No (Shake) So, it is the only possible tree, right? (Smile)
 
  • #20
evinda said:
No (Shake) So, it is the only possible tree, right? (Smile)

Yes! (Nod)
 
  • #21
I like Serena said:
Yes! (Nod)

Nice, thank you very much! (Smirk)
 

Similar threads

MHB Find Next Smallest & Greatest Key in BST
  • · Replies 1 ·
Replies
1
Views
2K
MHB Understanding Heaps & Deleting Elements
  • · Replies 9 ·
Replies
9
Views
2K
MHB Finding Depth & Height of Node w/ Key $r$ in $\text{AVL tree}$
  • · Replies 15 ·
Replies
15
Views
3K
MHB How do you draw a binary tree using pre-order and in-order traversal?
  • · Replies 14 ·
Replies
14
Views
3K
MHB Union of Disjoint Sets with at Most k Sets - Algorithm
  • · Replies 2 ·
Replies
2
Views
2K
MHB How Can You Check if a Binary Tree Satisfies the Properties of a 2-3 Tree?
  • · Replies 3 ·
Replies
3
Views
2K
MHB How can we add a node in a tree?
  • · Replies 40 ·
2
Replies
40
Views
7K
Java How to Calculate Leaf Node Difference in a Binary Tree Using Recursion?
  • · Replies 6 ·
Replies
6
Views
8K
Algorithm for computing the depths of all the nodes of tree
  • · Replies 1 ·
Replies
1
Views
3K
MHB What is the Time Complexity of this Vertex Cover Algorithm?
  • · Replies 1 ·
Replies
1
Views
2K