wasi-uz-zaman
- 89
- 1
- TL;DR
- under symmetry SU and U groups are used to confirm invariance of certain quantities.
hi,
i have studied Standard Model for particle physics - at present it is described by three groups -
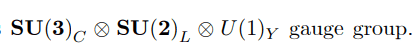
i have studied - these groups but could not establish what particular feature suggest of these group to be used to describe SM.
Thanks
i have studied Standard Model for particle physics - at present it is described by three groups -
i have studied - these groups but could not establish what particular feature suggest of these group to be used to describe SM.
Thanks