vcsharp2003
- 913
- 179
- Homework Statement
- I am trying to understand the paragraph mentioned below in my textbook. However, it doesn't make sense to me. The figure shown is Fig 10.19 (b) ( the other figure i.e. Fig 10.19 (b) is not shown).
- Relevant Equations
- None
I think in the explanation below a very small element of the liquid at the line of contact between the horizontal solid surface, air outside the liquid and the liquid itself is being taken, and forces acting on such a small element are being shown. This very small element is to the left of shown diagram. The liquid is going to have a circular area of contact with the solid surface and we have taken a very small arc element on the periphery of the liquid that is touching all three i.e. solid, liquid and air. I guess this part of my understanding is correct?
I cannot figure out how the liquid air force (##S_{la}##), solid air force (##S_{sa}##) and solid liquid force (##S_{la}##) point in the directions shown in the figure.

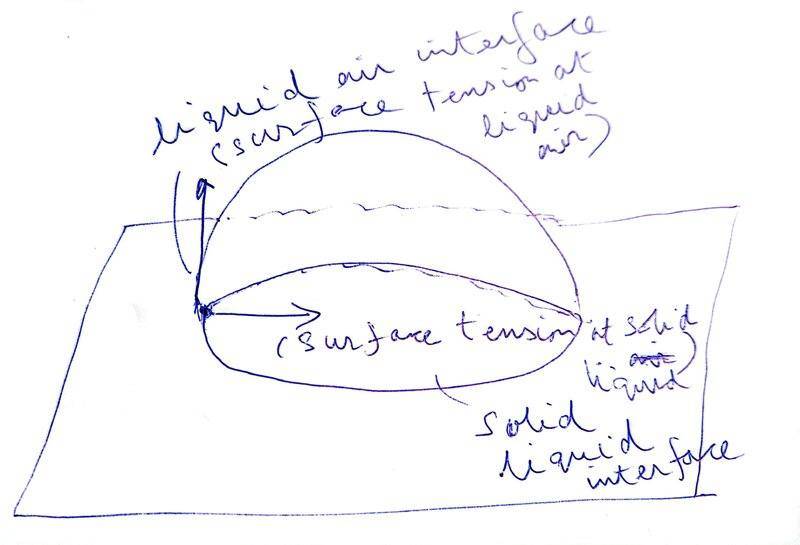
I cannot figure out how the liquid air force (##S_{la}##), solid air force (##S_{sa}##) and solid liquid force (##S_{la}##) point in the directions shown in the figure.
Attachments
Last edited: