Why are there only two roots of this cubic polynomial?

[PainterGuy]

Homework Statement

I'm not able to understand why I'm only getting two roots of cubic polynomial.

Relevant Equations

Please check my posting.

Hi,

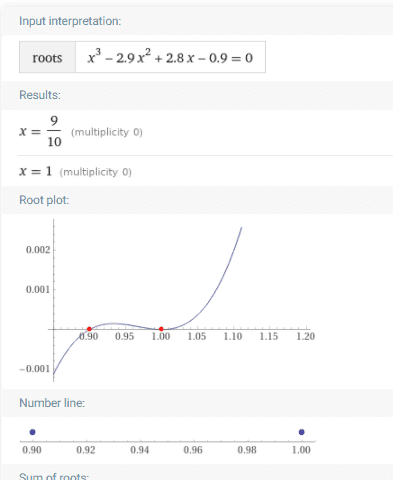
I was trying to find roots of the following cubic polynomial and there are only two roots. I believe there should be three roots. Could you please guide me why there are only two roots?

If you say that the "1" repeats itself as a root then I'd say the same could be said of "0.9". Thank you!

Source:
https://www.wolframalpha.com/input/?i=find+roots+x³-2.9x²%2B2.8x-0.9

 

[Office_Shredder]

Why do you think the same could be said of the 0.9 root?

 

[pasmith]

Try factorizing your cubic: $x^3 - 2.9x^2 + 2.8x - 0.9 = (x - 1)(x - 0.9)(x - a)$. What is $a$?

 

[PainterGuy]

Thank you!

a=1

 

[Office_Shredder]

If you look at the graph, at x=1 the graph bounces off the x-axis. This is how you can find double roots visually, if the graph bounces off the axis and doesn't pass through it it's a double root (or a root of multiplicity 4,6,8 etc.The two ways you can prove this to yourself:
One is the sign of the function doesn't change as you pass through a double root but it does as you pass through a single root (you should try to prove this to yourself)

The other more graphical way is that a double root should look a lot like two single roots right next to each other. If you graphed (x-0.9)(x-1.00001)(x-0.99999) you would not visually be able to distinguish those two roots, the graph would go under the x-axis and pop back up over it in a span too small for the naked eye. A double root should look visually the same as that.

 

[Mark44]

If you look at the graph, at x=1 the graph bounces off the x-axis. This is how you can find double roots visually, if the graph bounces off the axis and doesn't pass through it it's a double root (or a root of multiplicity 4,6,8 etc.

I second what Office Shredder has said. Another way to think about this is that near x = 1, the cubic polynomial is acting like a quadratic polynomial; i.e. one whose graph is a parabola.

In factored form, the equation is $y = (x - .9)(x - 1)^2$. If x is very close to 1, and hence relatively far from .9, the graph of the equation is $y \approx .1(x - 1)^2$. This graph is a parabola, with vertex at (1, 0) and opening upward. For x values farther away from 1, the x - .9 factor exerts more of an influence.

 

[FactChecker]

If you examined the graph under a microscope, the double root at x=1 looks and behaves like $c_1(x-1)^2$, so it touches the y=0 axis and goes back up. Under the same microscope, at the root x=0.9, the graph looks like $c_2(x-0.9)$, so it goes through the y=0 axis like a straight line. The two situations are not the same at all.