guyvsdcsniper
- 264
- 37
- Homework Statement
- Find the blocks acceleration on a wedge.
- Relevant Equations
- F=MA
I am currently solving this problem and approached it two different ways. I have attached a ss of the picture for reference.
On my first attempt, shown on the attached image in pen, I used a component of the normal force and weight as my forces in the y direction. I carried out the work and ended up getting the correct answer according to my book.
I then tried a different approach, as shown by the image with the whiteboard, and used the actual normal force and a component of the force of gravity. When I used this approach I got stuck and did not see anyway of attaining the correct answer.
What is incorrect about the 2nd approach that is preventing me from getting the right answer?
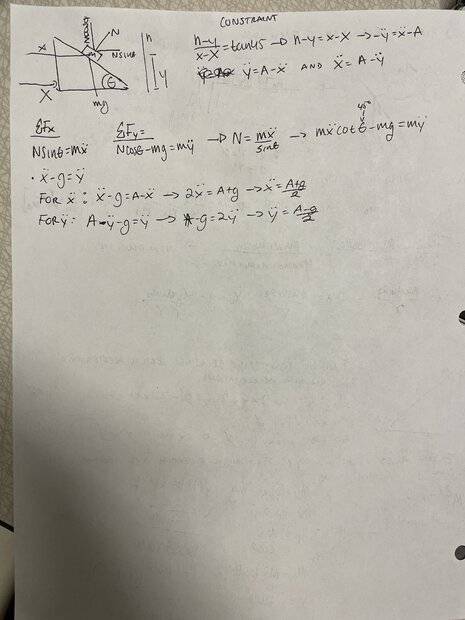


On my first attempt, shown on the attached image in pen, I used a component of the normal force and weight as my forces in the y direction. I carried out the work and ended up getting the correct answer according to my book.
I then tried a different approach, as shown by the image with the whiteboard, and used the actual normal force and a component of the force of gravity. When I used this approach I got stuck and did not see anyway of attaining the correct answer.
What is incorrect about the 2nd approach that is preventing me from getting the right answer?