Discussion Overview
The discussion revolves around the question of why multiplying different combinations of prime factors of a number results in all of that number's factors. The scope includes conceptual understanding of prime factorization and its implications for finding factors of composite numbers.
Discussion Character
- Conceptual clarification
- Debate/contested
Main Points Raised
- One participant explains that every composite number can be factored into products of prime numbers, suggesting that combinations of these prime factors yield composite factors of the original number.
- Another participant reiterates the need for an explanation of why multiplying combinations of prime factors results in all composite factors, emphasizing the inquiry into the underlying reasoning.
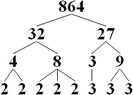
- A different participant provides a visual demonstration of the prime factorization process, illustrating that any composite factor can be broken down into its prime factors, which are part of the original number's prime factor list.
- This participant argues that since the list of prime factors remains consistent regardless of the composite factors chosen, any combination of these prime factors will produce any given composite factor.
Areas of Agreement / Disagreement
Participants express a shared understanding of the relationship between prime factors and composite factors, but there remains a lack of consensus on the deeper reasoning behind why this relationship holds true.
Contextual Notes
The discussion does not resolve the underlying question of why combinations of prime factors yield all factors of a number, leaving the reasoning open to further exploration.