BWV
- 1,640
- 1,992
Trying to get some better mathematical insight on why tax-deferred compounding of an investment has an advantage over annual taxation
so R=return, T=tax rate and n=time (years)
If the full return is taxed every year, a portfolio grows at:
(1+R(1-T))n
if the portfolio is only taxed at the end of the multi-year period, the value is:
((1+R)n-1)(1-T) +1 or, alternatively (1+R)n-(1+R)nT+T
For T >0 and R >0, and n > 1 the statement below is true, but not sure how I would prove it - Jenson's inequality perhaps?
(1+R(1-T))n < (1+R)n-(1+R)nT+T
If you plot the growth of the two portfolios, for 12% return and 24% tax rate, the values diverge dramatically:
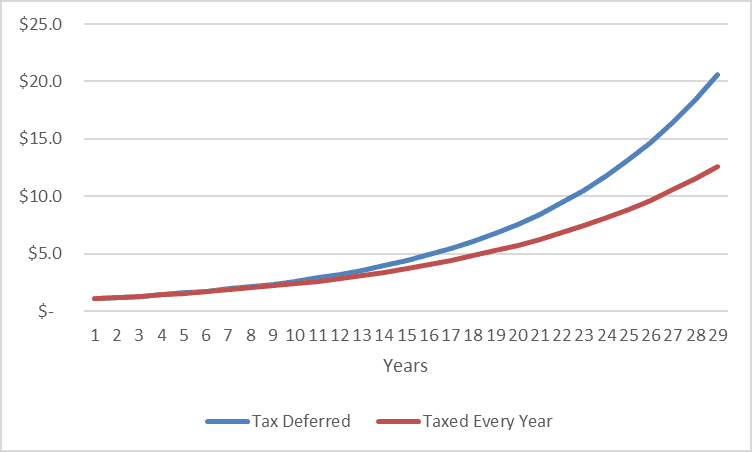
The y/y change on the 'Taxed every year' is simply (1+R(1-T)), however the 'Taxed Deferred' y/y change begins at (1+R(1-T)) but converges over time to (1+R) (at about 50 years in this example), - would like to understand this - taking derivatives with respect to n does not help much as you just get a log(1+r)(1+r)^n terms for both functions.
so R=return, T=tax rate and n=time (years)
If the full return is taxed every year, a portfolio grows at:
(1+R(1-T))n
if the portfolio is only taxed at the end of the multi-year period, the value is:
((1+R)n-1)(1-T) +1 or, alternatively (1+R)n-(1+R)nT+T
For T >0 and R >0, and n > 1 the statement below is true, but not sure how I would prove it - Jenson's inequality perhaps?
(1+R(1-T))n < (1+R)n-(1+R)nT+T
If you plot the growth of the two portfolios, for 12% return and 24% tax rate, the values diverge dramatically:
The y/y change on the 'Taxed every year' is simply (1+R(1-T)), however the 'Taxed Deferred' y/y change begins at (1+R(1-T)) but converges over time to (1+R) (at about 50 years in this example), - would like to understand this - taking derivatives with respect to n does not help much as you just get a log(1+r)(1+r)^n terms for both functions.