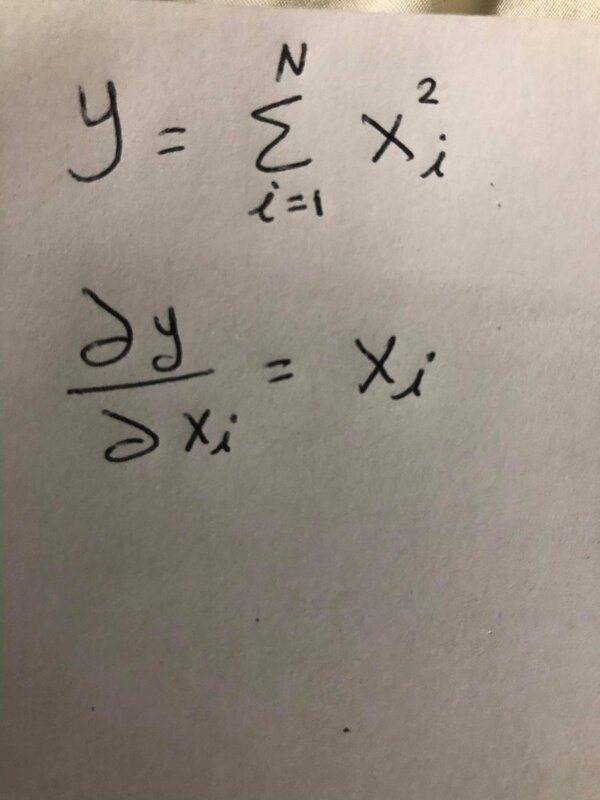Discussion Overview
The discussion revolves around the behavior of partial derivatives applied to a summation of functions, specifically focusing on why certain terms cancel out when differentiating with respect to a specific variable, denoted as x_i. Participants explore the implications of treating x_i as an independent variable and the mathematical reasoning behind the differentiation process.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant questions why the summation cancels out when taking the partial derivative with respect to x_i, suggesting a need for detailed explanation.
- Another participant asserts that if x_i are independent variables, then the derivative of x_j with respect to x_i is zero for j not equal to i, leading to a proposed answer of 2x_i.
- Some participants express confusion about the cancellation of terms in the summation and request further clarification on the differentiation process.
- A participant suggests using a different dummy variable for clarity in the summation limits.
- Multiple participants illustrate the differentiation process by expanding the summation and applying the derivative term by term, emphasizing that only the term corresponding to x_i contributes to the derivative.
- There is a discussion about the distinction between the specific index i and the summation index, with some participants clarifying that i refers to a specific variable while the summation runs over all variables.
- One participant expresses gratitude for the explanations and acknowledges their learning experience in the forum.
Areas of Agreement / Disagreement
Participants generally agree on the mechanics of differentiation in this context, but there is some confusion regarding the implications of the summation and the role of the indices. The discussion remains somewhat unresolved as participants clarify their understanding without reaching a definitive consensus on all points.
Contextual Notes
Some participants express uncertainty about the cancellation of terms and the treatment of indices, indicating a need for clearer definitions and assumptions regarding the variables involved in the summation.