Why is radius important in tension calculations but not in force components?

  • Thread starter Thread starter Godawgs94
  • Start date Start date
Click For Summary
The discussion centers on the significance of radius in tension calculations versus its absence in force component calculations. A uniform boom, supported by a cable and subject to a weight, raises questions about the role of radius in determining tension. Users express confusion over why radius is critical for tension but not for calculating hinge reaction forces. The importance of visual aids, like diagrams, is highlighted to clarify these concepts. Overall, understanding the mechanics behind these calculations is essential for accurate problem-solving in physics.
Godawgs94
Messages
3
Reaction score
0
A 1130 N uniform boom is supported by a cable perpendicular to the boom, as seen in the figure below.
The boom is hinged at the bottom, and an m = 1870 N weight hangs from its top. Assume the angles to be
mimetex.gif
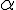= 69.5o and
mimetex.gif
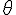= 90.0o -
mimetex.gif
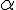. Find the tension in the supporting cable
Find the x-components of the reaction force exerted on the boom by the hinge (choose to the right as positive).
Find the y-components of the reaction force exerted on the boom by the hinge (choose upwards as positive).

I don't understand why radius is taken into account when calculating tension, but doesn't play a role in calculating the components of force.
 
Physics news on Phys.org
It would help to see the picture.
 
https://spock.physast.uga.edu/res/brookscole/serway/College_Physics_7ed/Chap08/graphics/serw0822.gifhttps://spock.physast.uga.edu/res/brookscole/serway/College_Physics_7ed/Chap08/graphics/serw0822.gif
sorry, here it is
 
Last edited:
axmls said:
It would help to see the picture.

picture is here

https://spock.physast.uga.edu/res/brookscole/serway/College_Physics_7ed/Chap08/graphics/serw0822.gif
 
Godawgs94 said:
picture is here

https://spock.physast.uga.edu/res/brookscole/serway/College_Physics_7ed/Chap08/graphics/serw0822.gif

Sorry, this link asks for your login information.

Please try to re-post your images.
 
Thread 'Correct statement about size of wire to produce larger extension'

Thread 'Correct statement about size of wire to produce larger extension'

The answer is (B) but I don't really understand why. Based on formula of Young Modulus: $$x=\frac{FL}{AE}$$ The second wire made of the same material so it means they have same Young Modulus. Larger extension means larger value of ##x## so to get larger value of ##x## we can increase ##F## and ##L## and decrease ##A## I am not sure whether there is change in ##F## for first and second wire so I will just assume ##F## does not change. It leaves (B) and (C) as possible options so why is (C)...
View full post »

Similar threads

Finding tension and reaction force for a boom
  • · Replies 1 ·
Replies
1
Views
6K
Finding tension force and and components of a uniform boom
  • · Replies 1 ·
Replies
1
Views
4K
Statics:Find the Tension in a rope holding a boom
  • · Replies 4 ·
Replies
4
Views
5K
Torque biomechanics
  • · Replies 6 ·
Replies
6
Views
2K
Time it Takes for a Transverse Pulse to Travel a Distance "L" Up a Cable Against Gravity?
  • · Replies 13 ·
Replies
13
Views
1K
Vector multiplication in static equilibrium
  • · Replies 4 ·
Replies
4
Views
2K
MHB Can You Solve for Tension and Force in Static Equilibrium for a Boom?
  • · Replies 2 ·
Replies
2
Views
3K
Flag pole finding horizontal force component at hinge.
  • · Replies 1 ·
Replies
1
Views
3K
Torque and rotational equilibrium question
  • · Replies 6 ·
Replies
6
Views
4K
Removing a crane cylinder, force calculation
  • · Replies 3 ·
Replies
3
Views
3K