Why Is the Correct Reflection of y=e^x About y=2 Given by y=4-e^x?

[brycenrg]

Homework Statement

Consider the graph y = e^x

Homework Equations

Make an equation that results in reflecting about the line y = 2

The Attempt at a Solution

I came up with 2 - e^x

And when I put it in my calculator it makes sense.
Just -e^x is reflected among y = 0
so if you bring it up 2, to y = 2 then it will be reflected among y = 2.
My webassign says I am incorrect and its actually 4 - e^x, why is this? I don't understand the logic

 

[Simon Bridge]

My webassign says I am incorrect and its actually 4 - e^x, why is this? I don't understand the logic

No logic has been presented so that is not too surprising.

Did you try plotting the graphs and the mirror-line to see?

Probably you got it different from them because you missed something out - but I cannot tell.
The bits where you say "reflected among" makes no sense to me.
Please show your working, and reasoning.

I suspect you forgot the second shift of two units after you did the reflection.

 

[brycenrg]

I'm apologize for the inefficient communication.

3. My Attempt

I start with e^x which is a curve that follows y=0 then starts to rise more abruptly at x=0

If - f(x) Makes you reflect over the x-axis

Then - e^x will do a neccesary reflection for reflecting it about y = 2

Then I add +2 to the end of f(x) = -(e^x)+2 = 2-e^x

Although on my homework they say the correct answer is 4 - e^x

Saying I needed to time 2 for some reason, which is where I lose understanding.

 

[Mentallic]

Make an equation that results in reflecting about the line y = 2

Let $f(x)=e^x$ and g(x) denote the function we're looking for. When we reflect about the line y=2, what we're saying is that we want $$2-f(x)=g(x)-2$$ to be true for all values of x that are in the domain of f(x). So when f(x) = 2, g(x) = 2. Your equation $g(x)=2-e^x$ is actually a reflection of f(x) in the line y=1.

 

[brycenrg]

Thanks for the reply, but I still don't understand.

Doesn't - f(x) reflect over the x-axis.

So let's say I had f(x) = x^2 (using x^2, because its easier to see on my calculator where it reflects)

If I put -f(x) = -x^2 that would just reflect it over y=0 so the origin.

And adding two to -x^2 + 2 would just raise it up to the reflect line which is asked for.

Isn't that the same for a equation like e^x or any other form of f(x)

 

[Mentallic]

Say you have the function f(x)=0 (the x-axis) and you want to reflect this function in the line y=2. Would your answer be g(x)=2? No, because g(x)=2 is on the line of reflection. You want g(x) to be the same distance above y=2 as f(x) is below y=2. So you're looking for g(x)=4.

Look back the distance equation I gave you:

$$2-f(x)=g(x)-2$$

Does this make intuitive sense to you?

If we rearrange the equation to solve for g(x), we get

$$g(x)=4-f(x)$$

That looks familiar, right?

Yes, $-e^x$ is a reflection in the x-axis, and yes, $2+(-e^x)=2-e^x$ will shift the function up 2 units, but this doesn't mean it's a reflection in the line y=2. Draw it out and understand that you want a function that reproduces f(x) below y=2 to another function g(x) above y=2. And vice versa, if f(x) is above y=2, then g(x) is below.

 

[brycenrg]

WOOO lol wow.

Yes Thank you Mentallic! Your explanation gave me the little mental push. Much appreciated :)

 

[Mentallic]

WOOO lol wow.

Yes Thank you Mentallic! Your explanation gave me the little mental push. Much appreciated :)

You're welcome And you can always extend this problem to shifting along any line y=a.

$$a-f(x)=g(x)-a$$

$$g(x)=2a-f(x)$$

 

[Simon Bridge]

Hmmm - you missed off a step all right.
You forgot to translate back.

Probably best if I just show you with your own example.
Say you - to reflect $f(x)=x^2$ about $y=1$, would give you $g(x)=1-x^2$

Here it is:

... the blue curve is y=x²
... the red line is y=1: the mirror line
... the green line is y=1-x²

Notice how the green line is NOT the blue line reflected about the red one?
Easy test: put a small mirror on the red line and check.

Can you see what the correct reflected function is now?

 

[brycenrg]

Thank you Simon Bridge, that helps a lot. I appreciate your help. :)

 

[Simon Bridge]

No worries.

It's usually easier to work these things out with pictures than algebra ... in future, try sketching the graphs out to check your work instead of just using single values on your calculator.

 

[Mentallic]

It's usually easier to work these things out with pictures than algebra

I agree. If only creating pictures were as easy as writing down the algebra...

 

[Simon Bridge]

... as we have just seen, making the pics is actually easier than writing down the correct algebra from off the top of one's head. OTOH: it is more labor-intensive to present a pic in this medium. Wolfram has an online mini-mathematica doesn't it? But what we really need is to get the output into a pic for presentation here.

What's cool about this place is that if I provide one approach, someone else tends to provide the other one.
So cheers :)

[edit]... note for those googling here in future:
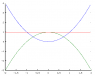
It is usually easier to see what's going wrong if you can plot the graph.
Not everyone has GNU-Octave, Matlab or Mathematica - or the need for that kind of power all the time.

Wolfram has a widget for simple plots:
http://www.wolframalpha.com/widget/...le=Math Help Boards: Graph Plotter&theme=blue

It will let you plot more than one graph on the same axis too:
i.e.
expression: x^2, 1, 1-x^2
from: -2
to: 2

... will give you the same graph I presented above.

If you enter: e^x, 2, 2-e^x, 4-e^(x) for the expression, then you get to compare the different examples in post #1.

A simple algebraic test that would catch the above mistakes: consider - if the graph crosses the mirror line, then the reflection will also cross the mirror line in the same places.