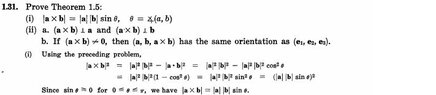Discussion Overview
The discussion revolves around the restriction of the angle $\theta$ to the interval $[0, \pi]$ in mathematics and physics, particularly in the context of vector angles and their properties. Participants explore the implications of this restriction, including its mathematical and physical interpretations.
Discussion Character
- Conceptual clarification
- Debate/contested
- Technical explanation
Main Points Raised
- Some participants propose that the sine function $\sin(\theta)$ is nonnegative in the interval $[0, \pi]$, which is relevant for defining the cross product's orientation.
- Others argue that the angle between two vectors is defined to be between $0$ and $\pi$, where $0$ indicates coinciding vectors and $\pi$ indicates opposite vectors.
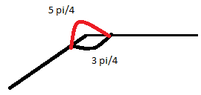
- A participant questions why angles like $\frac{5\pi}{4}$ are not considered, suggesting that they are effectively the same as angles like $\frac{3\pi}{4}$, emphasizing the convention of using the smallest applicable angle.
- Another participant illustrates that when considering angles between lines or vectors, the angle is always taken to be less than or equal to $\pi$, using a visual example to clarify this point.
- There is a mention of the periodic nature of angles, with a participant noting that angles like $\frac{3\pi}{4}$ can be equivalent to angles like $\frac{11\pi}{4}$, but the convention remains to refer to the smaller angle.
- A later reply discusses the distinction between mathematical angles (considered distinct in the interval $[0, 2\pi]$) and physical angles (often treated as directionless), suggesting a middle path of using angles in the interval $(-\pi, \pi]$ for physical interpretations.
- One participant highlights the ambiguity in defining angles based on orientation and the arbitrary nature of assigning signs to certain quantities in the physical world.
Areas of Agreement / Disagreement
Participants express multiple competing views regarding the treatment of angles in mathematics versus physics, and the discussion remains unresolved on certain aspects, particularly concerning the implications of angle orientation and the definitions used.
Contextual Notes
There are limitations regarding the assumptions made about angle definitions and the dependence on context (mathematical versus physical). The discussion does not resolve the ambiguities related to orientation and the assignment of signs to angles.