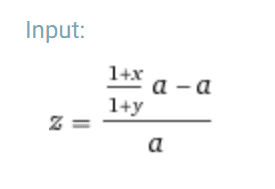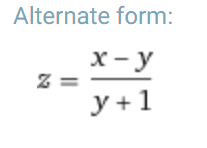SUMMARY
The discussion centers on simplifying the algebraic fraction \(\frac{(x+1)}{(y+1)} - 1\). Participants emphasize the importance of dividing both the numerator and denominator by \(a\) to reach the alternate form. Key techniques include reducing to a common denominator and recognizing that \(-1\) can be expressed as \(-\frac{(y+1)}{(y+1)}\). The conversation highlights common pitfalls in algebraic simplification and the value of collaborative problem-solving.
PREREQUISITES
- Understanding of algebraic fractions
- Familiarity with simplifying expressions
- Knowledge of common denominators
- Basic operations with rational expressions
NEXT STEPS
- Study the process of simplifying algebraic fractions
- Learn about reducing expressions to a common denominator
- Explore the properties of rational expressions in algebra
- Practice problems involving algebraic fraction simplification
USEFUL FOR
Students, educators, and anyone seeking to improve their skills in algebraic fraction simplification and rational expressions.