Why Must Any 2-Cycle of the 2D Torus Be of the Form pγ?

[Math Amateur]

I am reading James Munkres' book, Elements of Algebraic Topology.

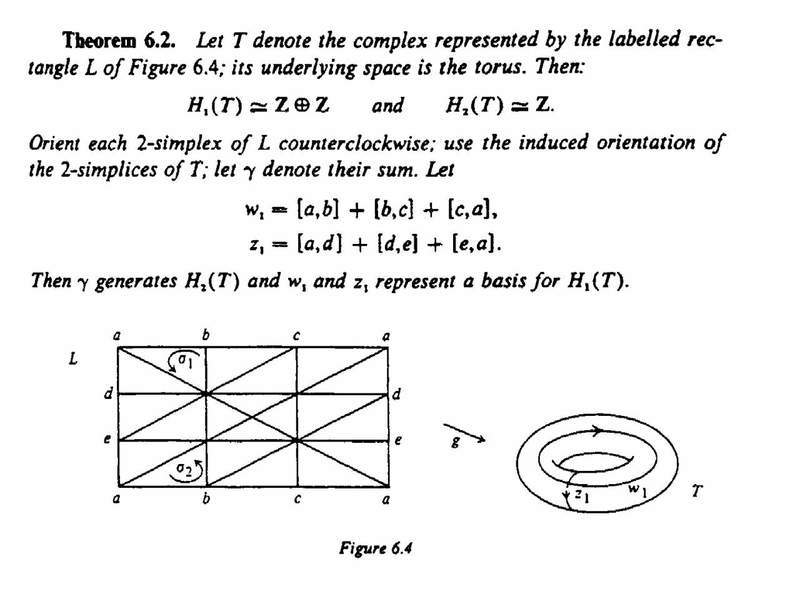
Theorem 6.2 on page 35 concerns the homology groups of the 2-dimensional torus.

Munkres shows that $H_1 (T) \simeq \mathbb{Z} \oplus \mathbb{Z}$ and $H_2 (T) \simeq \mathbb{Z}$.

After some work I now (just!) follow the proof that $H_1 (T) \simeq \mathbb{Z} \oplus \mathbb{Z}$ but I need some help to understand a point in the proof of $H_2 (T) \simeq \mathbb{Z}$.

Munkres' argument to show $H_2 (T) \simeq \mathbb{Z}$ is as follows:

-----------------------------------------------------------------------------

To compute $H_2 (T)$, note that by (2) any 2-cycle d of T must be of the form $p \gamma$ for some p. Each such 2-chain is in fact a cycle,by (4) , and there are no 3-chains for it to bound. We conclude that

$H_2 (T) \simeq \mathbb{Z}$

and this group has as generator the 2-cycle $\gamma$.

------------------------------------------------------------------------------------------------


I do not fully understand why any 2-cycle d of T must be of the form $$p \gamma$$ for some p.

Can someone please explain exactly why this follows?

Would appreciate some help.



-----------------------------------------------------------------------------


To give members of the Physics Forums the context of the post above, the text of Theorem 6.2 and its proof follow:

Some of my thoughts ... ...

Basically, to show that any 2-cyclce of L (i.e. T) os of the form $$ p \gamma $$, we have to show the following:

If $d = \sum_i n_i \sigma_i$ where $\partial d = 0$ then $d = p \gamma$.

We have, of course that $\gamma = \sum_i \sigma_i$

Note that we have that if d is a 2-chain of L and if $\partial d$ is carried by A then d is a multiple of $\gamma$.

Munkres defines 'carried by' in the following text taken from page 31:

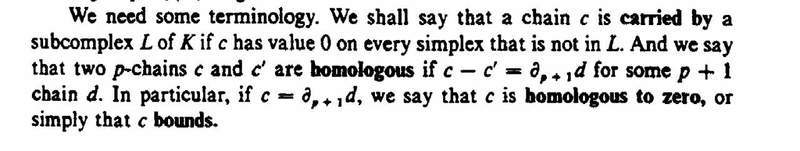
Hope someone can help.

Peter

 

[micromass]

Take a $2$-cycle $d$. Then obviously $d$ is a $2$-chain. And also by definition of $2$-cycle, we have $\partial d = 0$. In particular, $\partial d$ is carried by $L$. Thus $(2)$ implies that $d$ is a multiple of $\gamma$, which means by definition that $d=p\gamma$ for some $p$.

 

[Math Amateur]

Thanks micromass ...

OK so we take a 2-cycle d ... but how do we know that an arbitrary 2-cycle is carried by L?

BTW ...Do you mean carried by L or A? If as I suspect you mean A ... then ... how do we know that an arbitrary cycle is carried by A ... this is exactly my problem ...

Again, thanks for you prompt help

Peter

 

[micromass]

Thanks micromass ...

OK so we take a 2-cycle d ... but how do we know that an arbitrary 2-cycle is carried by L?

BTW ...Do you mean carried by L or A? If as I suspect you mean A ... then ... how do we know that an arbitrary cycle is carried by A ... this is exactly my problem ...

Again, thanks for you prompt help

Peter

I meant $A$. And we don't need to show that an arbitrary cycle is carried by $A$ (I doubt it's even true). To apply $(2)$, we need to show that for any cycle $d$, we have that $\partial d$ is carried by $A$. This is what we need to show. But $\partial d = 0$ by definition of a cycle. And of course $0$ is carried by $A$.

 

[Math Amateur]

Thanks so much ... that clears up that matter and gives me the confidence to go on ...

Thanks again,

Peter