Hernaner28
- 261
- 0
Hi. This is not actually not part of the homework; but it's something I'd like to do.
I have to solve the following system using Newton-Raphson's method:
$$\begin{matrix}
\frac{X}{\mu }+Y=1 \\
X=\left( \lambda -\left( K-1 \right)X \right)Y \\
\end{matrix}$$
Surfing the internet I found this precious Wolfram Demonstration:
http://demonstrations.wolfram.com/IterationsOfNewtonsMethodForTwoNonlinearEquations/
which is an interactive plot where you can select the starting point and see how and where it converges.
So I took the code and put those functions of mine:
It uses the FindRoot command which is supposed to use Newton's method but it actually does not purely. I checked this because I wrote the method on Octave and the region of convergence is the following:
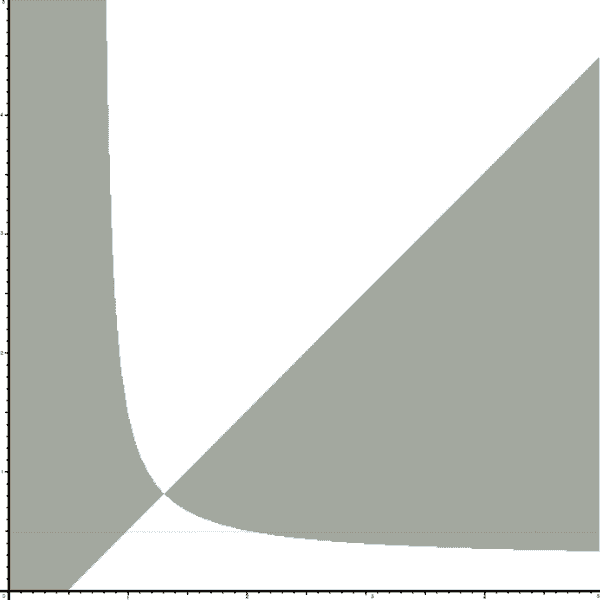
As you can see it's "solid" whereas in the Wolfram Demonstration you can see stripes so FindRoot clearly does not use Newton's method.
So now I want to replace that FindRoot command to match the existing code but using the pure Newton's method. I just don't know where to start because I barely understand that code.
So if someone is a pro in Wolfram I would really appreciate him/her !
I have to solve the following system using Newton-Raphson's method:
$$\begin{matrix}
\frac{X}{\mu }+Y=1 \\
X=\left( \lambda -\left( K-1 \right)X \right)Y \\
\end{matrix}$$
Surfing the internet I found this precious Wolfram Demonstration:
http://demonstrations.wolfram.com/IterationsOfNewtonsMethodForTwoNonlinearEquations/
which is an interactive plot where you can select the starting point and see how and where it converges.
So I took the code and put those functions of mine:
Code:
Manipulate[
Quiet@DynamicModule[{sol},
sol = Prepend[
Reap[FindRoot[f, {vars, start}\[Transpose],
StepMonitor :> Sow[vars]]][[2, 1]], start];
Show[g1, g2,
Graphics[{PointSize[Medium], Point[sol], Thickness[Medium],
Line[sol], Style[Text[start, {-20, 20}, {-1, 1}], 12]}]]],
{{start, {3.7, 5.7}}, Locator},
SaveDefinitions -> True,
SynchronousInitialization -> False,
TrackedSymbols -> True,
Initialization :> {
f = {x + y - 1, x - y*(0.99 - 4*x) },
vars = {x, y},
root = vars /. FindRoot[f, {vars, {1, 1}}\[Transpose]],
pp = {},
Do[sol = vars /. FindRoot[f, {vars, {x0, y0}}\[Transpose]];
If[Norm[sol - root] < 10^-7, pp = {pp, {x0, y0}}], {x0, -20,
20, .12}, {y0, -20, 20, .12}],
g1 = ListPlot[Partition[Flatten[pp], 2], AspectRatio -> Automatic,
PlotStyle -> PointSize[Tiny],
PlotRange -> {{-20, 20}, {-20, 20}},
Ticks -> {Range[-20, 20], Range[-20, 20]},
ImageSize -> {480, 480}],
g2 = ContourPlot[
Evaluate[Thread[f == 0]], {x, -20, 20}, {y, -20, 20},
ContourStyle -> {{Thick, Green}, {Thick, Orange}}]}]It uses the FindRoot command which is supposed to use Newton's method but it actually does not purely. I checked this because I wrote the method on Octave and the region of convergence is the following:
As you can see it's "solid" whereas in the Wolfram Demonstration you can see stripes so FindRoot clearly does not use Newton's method.
So now I want to replace that FindRoot command to match the existing code but using the pure Newton's method. I just don't know where to start because I barely understand that code.
So if someone is a pro in Wolfram I would really appreciate him/her !
![convergencia[0,5]x[0,5] a 0.01.png](/data/attachments/48/48120-db66ab9470080ee5789f3488b929de2f.jpg?hash=22arlHAIDu)