MyoPhilosopher
- 41
- 4
- Homework Statement
- Work done by a force along the path
- Relevant Equations
- \vec F(\vec r)=α|\ vec r 2 \vecr.
r(s)=sˆx+sˆy,
If the first equation for force is not formatted please refer to the pic.
I did not post my full attempt as the problematic equation leads to a complex integral.
Should I be converting r vector into its univector. The two outlined equations refer to the force. I am making an error transforming the force into x_hat and y_hat format. Any advice is appreciated I am quite stuck
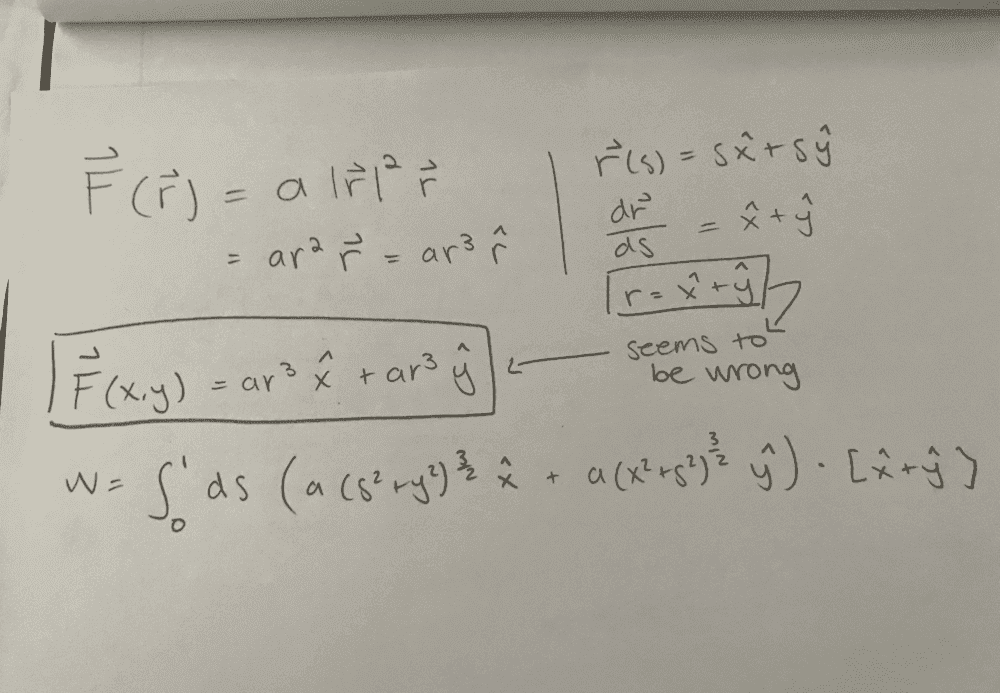
I did not post my full attempt as the problematic equation leads to a complex integral.
Should I be converting r vector into its univector. The two outlined equations refer to the force. I am making an error transforming the force into x_hat and y_hat format. Any advice is appreciated I am quite stuck