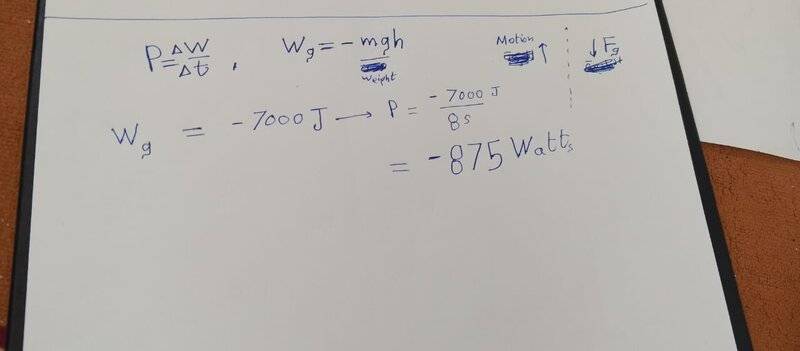Homework Help Overview
The discussion revolves around the concept of work done by gravity in the context of a man climbing upwards. Participants explore the implications of positive and negative work, particularly in relation to gravitational force and potential energy changes.
Discussion Character
- Conceptual clarification, Assumption checking, Mixed
Approaches and Questions Raised
- Some participants question why work done by gravity is considered positive in certain contexts, while others discuss the relationship between work, power, and potential energy. There are attempts to clarify the definitions of positive and negative work in relation to the forces involved.
Discussion Status
The discussion is active, with participants providing insights into the mechanics of work and energy transfer. There is an exploration of different interpretations regarding the signs associated with work done by gravity and the lifting force. Some participants express confusion about specific conclusions drawn in the discussion.
Contextual Notes
Participants note the importance of specifying the forces involved when discussing work. There is an emphasis on the conditions under which work is considered positive or negative, particularly in the context of gravitational potential energy and the work-energy theorem.