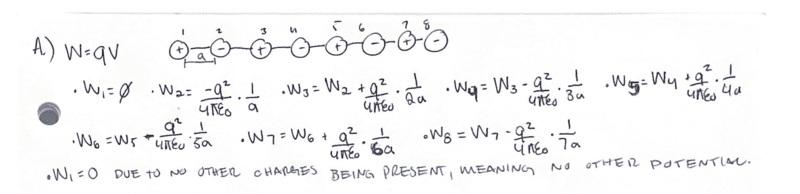SUMMARY
The discussion focuses on calculating the work per particle in an infinite NaCl chain, specifically addressing the interaction energies between ions. The key formula involves the sum of interaction energies, represented as ##U(0,1) + U(-1,0) + U(0,2) + U(-2,0) + \dots##, which leads to the total energy per particle being proportional to ##\sum\limits_{\substack{m,n \\ m
PREREQUISITES
- Understanding of ionic interactions and potential energy in solid-state physics.
- Familiarity with series expansions, particularly the series expansion of ##ln(2)##.
- Knowledge of electrostatic principles, specifically Coulomb's law and its applications.
- Basic skills in mathematical summation and manipulation of infinite series.
NEXT STEPS
- Study the derivation and implications of Coulomb's law in ionic compounds.
- Learn about series expansions and their applications in physics, focusing on logarithmic functions.
- Explore the concept of energy per particle in infinite systems, particularly in solid-state physics.
- Investigate methods to avoid double counting in summation problems involving infinite series.
USEFUL FOR
Students and researchers in solid-state physics, chemists studying ionic compounds, and anyone interested in the thermodynamic properties of materials.