rede96
- 663
- 16
Hi, I was hoping someone could help me figure out the problem below. It is a bit of a long winded questions so please bare with me!
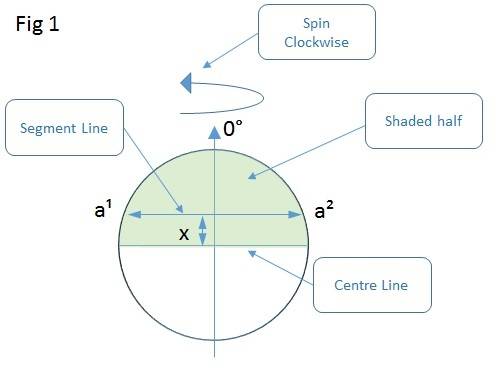
If you look at Fig 1 below, I have a sphere that spins about an axis in a clockwise direction. (the direction of the spin doesn't really matter) In this case the axis is pointing directly upwards, so the angle is 0 degrees.
You will notice the sphere also has a shaded area which covers the top half of the sphere.
If a put a 'segment line' perpendicular to the axis, which is at a distance x from the centre line, it will intersect the surface of the sphere at 2 points which I have labelled a1 and a2.
I know that as long as I place the segment line above the centre line then points a1 and a2 will always be in the shaded area as the sphere rotates.
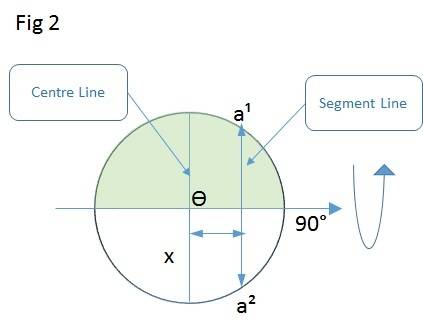
Now if I turn the axis by 90 degrees as in Fig 2 below, I can put a segment line at any distance x from the centre line, perpendicular to the axis, and points a1 and a2 will spend 50% of the time in the shaded area and 50% of the time in the unshaded area, as the shaded area doesn't rotate with the axis.
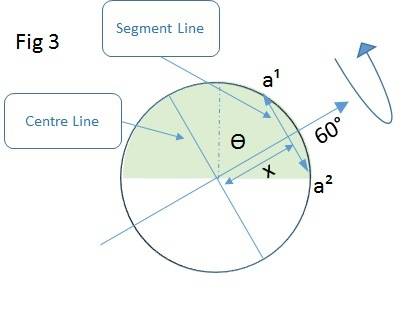
So, I now turn the axis to 60 degrees as in Fig 3 below and I want to know at what distance x would the segment line need to be away from the centre line so points a1 and a2 would always be in the shaded area as the sphere turns.
I can do a bit of trig here and make a right angled triangle between the centre point of the circle, point a2 and the point where the segment line intersects the axis. I know the angle is 30 degrees and I know the radius r, so Cos 30 r = x
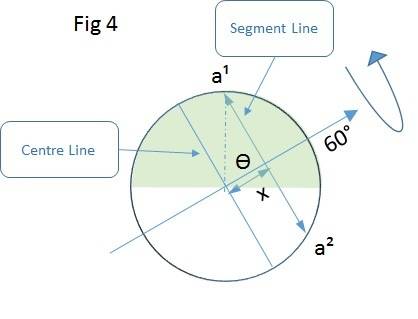
In Fig 4 below the axis is again at 60 degrees. My question is at what distance x from the centre line would I need to place the segment line so points a1 and a2 would spend 75% of the time in the shaded area and 25% of the time in the unshaded area as the sphere rotates. I just can't figure this out!
Any help would be much appreciated.
If you look at Fig 1 below, I have a sphere that spins about an axis in a clockwise direction. (the direction of the spin doesn't really matter) In this case the axis is pointing directly upwards, so the angle is 0 degrees.
You will notice the sphere also has a shaded area which covers the top half of the sphere.
If a put a 'segment line' perpendicular to the axis, which is at a distance x from the centre line, it will intersect the surface of the sphere at 2 points which I have labelled a1 and a2.
I know that as long as I place the segment line above the centre line then points a1 and a2 will always be in the shaded area as the sphere rotates.
Now if I turn the axis by 90 degrees as in Fig 2 below, I can put a segment line at any distance x from the centre line, perpendicular to the axis, and points a1 and a2 will spend 50% of the time in the shaded area and 50% of the time in the unshaded area, as the shaded area doesn't rotate with the axis.
So, I now turn the axis to 60 degrees as in Fig 3 below and I want to know at what distance x would the segment line need to be away from the centre line so points a1 and a2 would always be in the shaded area as the sphere turns.
I can do a bit of trig here and make a right angled triangle between the centre point of the circle, point a2 and the point where the segment line intersects the axis. I know the angle is 30 degrees and I know the radius r, so Cos 30 r = x
In Fig 4 below the axis is again at 60 degrees. My question is at what distance x from the centre line would I need to place the segment line so points a1 and a2 would spend 75% of the time in the shaded area and 25% of the time in the unshaded area as the sphere rotates. I just can't figure this out!
Any help would be much appreciated.
Last edited: