Edward Barrow said:
One would assume Earths spin would slow down as the rogue planet approached, spin at its slowest rate when the rogue planet is right beside it, and then spin faster again once the rogue planet leaves the vicinity of Earth.
No, one wouldn't, or at least shouldn't, because that's not how it works.
Look at the picture below:
The top row depicts a static situation, where the smaller body raises a tidal bulge on the larger one (the opposite case is of little interest to us here).
The lower rows have the larger body rotating at angular velocity ω1, while the smaller body flies by at closest approach R, with instantaneous tangential velocity V, which translates to angular velocity ω2=V/R.
If the angular velocity of the planet's rotation is larger than the angular velocity of the rogue moon, then the tidal bulge is displaced forward, giving rise to a torque that is retarding the rotation.
If it's the angular velocity of the rogue moon that is larger, then the tidal bulge is displaced backward, and the moon's gravity produces torque on the bulge resulting in acceleration of the rotation.
Let's find out how far the rogue moon needs to pass by for one effect to win over the other.
If it's a rogue body, then it must have at least the escape velocity w/r to the Sun, which at Earth's orbital radius is approx 42 km/s. Earth's orbital velocity is 30 km/s, and the rogue body will have gained up to ~11 km/s falling into Earth's gravity well, so depending on the direction of approach, the minimum relative velocity is between ~80 and 20 km/s.
We are going to assume that the direction of approach w/r to the Earth's rotation is as shown in the first picture, and that the encounter happens in the plane of Earth's rotation.
Taking the lowest value, for ω2 to be larger than ω1 the body would have to pass Earth closer than R=V/ω1, where ω1 = 2π/(24*3600) rad/s. This gives approx 275 000 km, or a distance comparable to Lunar orbit.
This means, that the tidal interaction will have retarding effect on the rotation only when the rogue body is further than that. While it'll spend most of the time at such larger distances, its tidal effects on Earth will match that of the Moon only for a short time.
The reminder of the approach, where tidal effects are the strongest (remember, tidal acceleration scales with third power of distance), will accelerate Earth's rotation.
You could get deceleration (and only deceleration) if the body passed from the other side of Earth, so that their angular velocities have opposite directions.
Having said that, and reinforcing what mfb stressed, even at the Roche limit, a single passage of a Moon-like body would not produce enough torque to cause noticeable changes in day length of the magnitude you're envisioning. We're talking millions of years of constant tidal interactions here, not a few hours.
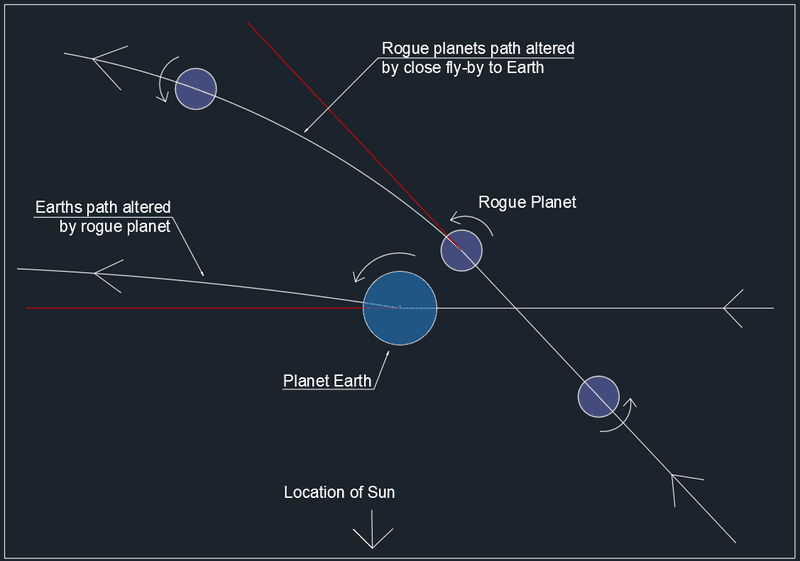
Edward Barrow said:
I presume the interaction would result in a slight change in Earth orbit around the sun, pulling it outwards. This is why I have drawn a new line for Earths orbit after the interaction.
This would make the length of a year on Earth longer I presume?
The way it's drawn, the interaction is a slingshot manoeuvre, where the smaller body 'steals' orbital momentum of the other body. It'd result in a boost for the rogue body, and a decrease in instantaneous orbital velocity of Earth. This in turn means that Earth's orbit would become more eccentric, with its perihelion distance going down and its orbital period reduced = shorter year. The deflection of the velocity direction is less important.