Write MATLAB code to find Y bus for any bus system

[Fatima Hasan]

Homework Statement

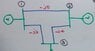
Write MATLAB code to find Y bus for any bus system, calculate Z, I, Bus voltages, and power of the following system (attached below).

Relevant Equations

-

Here's my work:

clc;
clear all;
% Ybus by step by step method for an any bus system

%         |  From |  To   |   R     |   X    |   gsh    |     B  |   T|ysh
%         |  Bus  | Bus   |  pu     |  pu    |    pu    |     pu   | ph-sh
linedata =  [1       2        0        -5         0          0        0
             1       3        0        -3         0          0        0
             2       3        0        -4         0          0        0];
        
fbus=linedata(:,1);             % Reading from bus
tbus=linedata(:,2);             % Reading to bus
R = linedata(:,3);              % Resistance, R...
X = linedata(:,4);              % Reactance, X...
gsh=linedata(:,5);
B = 1i*linedata(:,6);         % Ground Admittance, TOTAL..
T=linedata(:,7);
Z= R + 1i*X;                    % Z matrix...
y = 1./Z

buses = max(max(fbus),max(tbus));      % No. of buses...
lines = length(fbus);               % No. of elements...

%        Eg    Xg  Zd
BusData=[1     1   inf
        0      0   inf
        0      0   inf]   
 
Eg=BusData(:,1);
Xg=1i*BusData(:,2);
Zd=1i*BusData(:,3);
Zd=-1./Zd;
Xg=-Xg;   
ybus= zeros(buses,buses);       % Initializing YBUS as a zero matrix

for i=1:lines                % Forming the off diagonal elements
 if fbus(i)>0 && tbus(i)>0
     ybus(fbus(i),tbus(i))=ybus(fbus(i),tbus(i))-y(i);
    ybus(tbus(i),fbus(i))=ybus(fbus(i),tbus(i));     %same as opposite element
 end
endfor i=1:buses                   % Forming the diagonal elements
    for j=1:lines
        if fbus(j)==i || tbus(j)==i      % || represents  OR
            ysh(i,i)=(gsh(j)+B(j))/2;   
            ybus(i,i)=ybus(i,i)+y(j);   
        end
    end
end
yn=ybus+ysh+Xg+Zd   %Y
I=[Eg/Xg]           %I
Z=inv(yn)           % Z
V=inv(yn)*I         %Bus voltages

However, I got a different result from the corrected one (attached below). Could someone figure out my mistake please ?

 

[jedishrfu]

Its unreasonable to tell us:

I wrote this program and it doesn't work can you find my mistake?

You should instead use the MATLAB debugger and step through your code to see if its doing what you expect at every step.

Sadly, programmers must understand the algorithms they implement and be able to solve it manually in order to be able to debug their programs.

Work through your code and tell what line or lines you think its wrong. You can even put in print statements to show intermediate results and use the computer to compute some numbers to help you.