- #1
foo9008
- 676
- 4
Homework Statement
the answer that i found id 2(e^t) -1 , why it is wrong ? the answer given is cosht
Y" -y' -2y = 4(t^2) , y(0) = 1 , y'(0) =4?
- Thread starter foo9008
- Start date
Click For Summary
Homework Help Overview
The discussion revolves around a second-order linear differential equation with initial conditions. The original poster presents a solution they found, which differs from the expected answer provided in the context of the problem.
Discussion Character
- Exploratory, Assumption checking, Problem interpretation
Approaches and Questions Raised
- Participants question whether the original poster substituted their solution back into the original equation and whether it satisfied the initial conditions. There are discussions about the appropriateness of the thread title and the formulation of the problem statement. Some participants suggest that the problem may have been copied incorrectly, while others explore the use of the Laplace transform and the characteristic equation of the differential equation.
Discussion Status
The discussion is ongoing, with participants providing guidance on checking the validity of the proposed solutions and clarifying the problem's requirements. Multiple interpretations of the problem are being explored, particularly regarding the correct equation and the methods to solve it.
Contextual Notes
There is confusion regarding the equation presented in the thread title versus the one in the original post. Participants note that the initial value problem may not align with the differential equation stated in the title, which could affect the approach taken.
the answer that i found id 2(e^t) -1 , why it is wrong ? the answer given is cosht
- #2
SteamKing
Staff Emeritus
Science Advisor
Homework Helper
- 12,828
- 1,673
Did you substitute your answer back into the original differential equation? Did it satisfy this equation and all of the initial conditions?
If the answer is no, it didn't, then that's why.
BTW: You should not put one equation in the thread title when the problem covers a completely different equation.
If the answer is no, it didn't, then that's why.
BTW: You should not put one equation in the thread title when the problem covers a completely different equation.
- #3
Mark44
Mentor
- 38,093
- 10,644
Furthermore, the equation should be in the problem statement section, not in the thread title.SteamKing said:
- #4
LCKurtz
Science Advisor
Homework Helper
- 9,567
- 775
foo9008 said:Homework Statement
the answer that i found id 2(e^t) -1 , why it is wrong ? the answer given is cosht
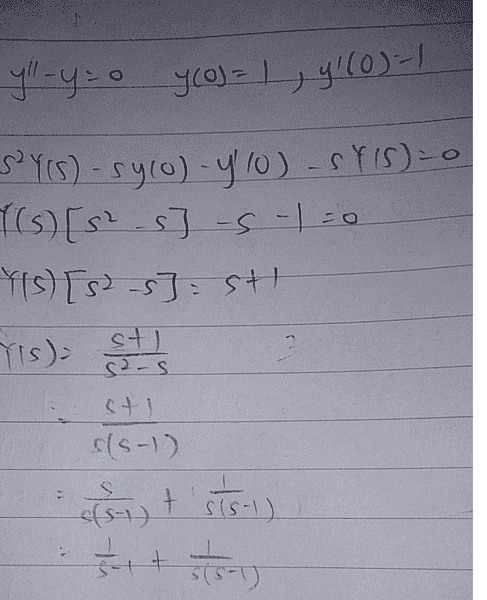
Homework Equations
The Attempt at a Solution
If you try your answer and the book's answer in the original equation, you will see both are incorrect. Either that, or you copied the problem incorrectly. In your work, ##\mathcal L(y) \ne s Y(s)##. Also, there is no reason to post this problem as an image instead of just typing it.
- #5
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 983
Are you required to use the Laplace transform? This is a simple second order, linear equation with constant coefficients. It has characteristic equation r^2- r- 2= (r- 2)(r+ 1) and a "specific solution" to the entire equation must be of the form Ax^2+ Bx+ C.
- #6
Mark44
Mentor
- 38,093
- 10,644
No. The DE in the title is different from the one in the image that the OP posted. The initial value problem in the posted image is y'' - y = 0, y(0) = 1, y'(0) = 1.HallsofIvy said:
- #7
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 983
Which is even easier without using the Laplace transform! The characteristic equation is r^2- 1= (r- 1)(r+ 1)= 0.
Similar threads
- · Replies 18 ·
- · Replies 4 ·
- · Replies 3 ·
- · Replies 10 ·