Young's Modulus; Extension of a wire

[AJKing]

Homework Statement

This is from A.P. French, Vibrations and Waves, Problem 3-7

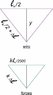
A wire of unstretched length l₀ is extended by a distance of 10^-3l₀ when a certain mass is hung from its bottom end. If this same wire is [turned to be horizontal] and the same mass is hung from the midpoint of the wire [...], what is the depression y of the midpoint, and what is the tension in the wire?

Homework Equations

F = -\frac{AY}{l_0}*x

F = k*x

k = -\frac{AY}{l_0}

The Attempt at a Solution

The correct answer is y = l₀ / 20
and T = 5 * mg

I have not recreated these solutions.

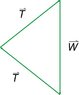
I have two triangles to consider:

one of lengths, with base l₀/2, height y and hypotenuse l₀ + x

one of Forces, with base T_i, height mg/2 and hypotenuse T = -\frac{AY}{l_0}*x

I've tried a lot of things. I'm missing something fundamental.
If you can get the correct answer, I would appreciate a little direction.

 

[Basic_Physics]

Wire extension

Does this make sense?
At this stage my answer seem to be out by a factor 2.

 

[AJKing]

For forces,

how did you get kl₀/2000 for the horizontal aspect?

 

[Chestermiller]

From the conditions on the vertical orientation of the wire, you get that

YA = 1000 mg

Let y represent the distance that the center of the wire moves down. Then, from the pythagorean theorem,
\left( \frac{l}{2}\right) ^2=\left( \frac{l_0}{2}\right) ^2+y^2
Solving for l/2:
\left( \frac{l}{2}\right) =\sqrt{\left( \frac{l_0}{2}\right) ^2+y^2}≈\left( \frac{l_0}{2}\right)+\frac{y^2}{l_0}
From this, strain=\frac{l/2-l_0/2}{l_0/2}=2\left(\frac{y}{l_0}\right)^2

Let T represent the tension in the wire. Force balance on hanging weight:
2T\frac{y}{l_0/2}=mg

How is the tension related to Y, A, and the strain in the wire?

 

[Basic_Physics]

1/2 mg = k l_o /1000

 

[Chestermiller]

1/2 mg = k l_o /1000

This is incorrect. We already showed before that YA=kl₀=1000 mg, based on the weight being in equilibrium when the weight is hung from the wire vertically. The question I was asking was, what is the general relation between the tension and strain, to wit:

T = YA (strain) = kl₀ (strain)

In the case of the horizontal wire, this gives

T = YA (2 (y/l₀)^2)=1000mg (2 (y/l₀)^2)

See what you get when you substitute this into the force balance.

 

[Basic_Physics]

Typo, I wanted to say

1/2 mg = k l_o /2000

This I concluded from the information given in the initial problem statement.
The 1/2 factor comes from the fact that only half of the magnitude of the weight is used for the base of the inverted right angled triangle in the force diagram. Do you agree with that?

 

[Chestermiller]

Typo, I wanted to say

1/2 mg = k l_o /2000

This I concluded from the information given in the initial problem statement.
The 1/2 factor comes from the fact that only half of the magnitude of the weight is used for the base of the inverted right angled triangle in the force diagram. Do you agree with that?

No. If this is the force balance for the weight hanging from the horizontal wire, then it is incorrect. From the free body diagram, if T is the tension in the wire, you have to determine the component of T in the vertical direction (see the force balance equation that I gave in my earlier post). Also, the strain and tension in the horizontal wire are not the same as in the vertical wire.

Chet

 

[Basic_Physics]

I used a vector diagram for the forces turned through 90^o
where W is the weight and T the tensions in the wire.
One can then use the fact that the two triangles are congruent to compare the ratio of the sides.

 

[Chestermiller]

This diagram is not what is described in the problem statement (for which the book solution and my solution apply). Think of a long horizontal clothesline from which you hang a small weight at the center.

 

[AJKing]

From the conditions on the vertical orientation of the wire, you get that

YA = 1000 mg

Let y represent the distance that the center of the wire moves down. Then, from the pythagorean theorem,
\left( \frac{l}{2}\right) ^2=\left( \frac{l_0}{2}\right) ^2+y^2
Solving for l/2:
\left( \frac{l}{2}\right) =\sqrt{\left( \frac{l_0}{2}\right) ^2+y^2}≈\left( \frac{l_0}{2}\right)+\frac{y^2}{l_0}
From this, strain=\frac{l/2-l_0/2}{l_0/2}=2\left(\frac{y}{l_0}\right)^2

Let T represent the tension in the wire. Force balance on hanging weight:
2T\frac{y}{l_0/2}=mg

How is the tension related to Y, A, and the strain in the wire?

Taylor expansions need to be more popular in my repertoire.
And using sinx = tanx was also wise.
These were stumbling points - certainly.

Using your approximations, I can easily calculate the Tension if I assume y = l₀/20
However, I'm still having problems calculating y.

May I have a less thorough suggestion?

 

[Chestermiller]

Taylor expansions need to be more popular in my repertoire.
And using sinx = tanx was also wise.
These were stumbling points - certainly.

Using your approximations, I can easily calculate the Tension if I assume y = l₀/20
However, I'm still having problems calculating y.

May I have a less thorough suggestion?

You are basically dealing with 3 key types of equations in this analysis:

1. The Strain-Displacement Equation
2. The Force Equilibrium Equation
3. The Stress Strain Equation

In the end, you will combine these three equations to get the solution to your problem.

Strain-Displacement Equation:
The Strain-Displacement Equation is a geometric equation which, in this problem, expresses the tensile strain ε in the wire as a function of the downward displacement at the center of the wire y. We already derived this relationship, and it is given by:
\epsilon=2\left(\frac{y}{l_0}\right)^2
Force-Equilibrium Equation:
This is the force balance on the weight, and expresses the tension in the wire T as a function of the displacement y. We already derived this relationship, and it is given by:
2T\left(\frac{y}{l_0/2}\right)=mg
Stress Strain Equation:
This is basically Hooke's law, and expresses the tension in the wire as a function of the tensile strain in the wire:
T=YA\epsilon
But, in Part I of the problem, we showed that, YA=1000mg
Therefore, for this problem, the Hooke's law relationship becomes:
T=1000mg\epsilon

Now, all you need to do is combine these three equations:
\epsilon=2\left(\frac{y}{l_0}\right)^2
2T\left(\frac{y}{l_0/2}\right)=mg
T=1000mg\epsilon

You do this by eliminating the tension T and the strain ε from the equations. See what you get when you do this.

 

[AJKing]

[...]

Damn.

I appreciate all the help. I've arrived at the right answer.
But, damn.

I did not do well on this question.

Thanks mate

 

[Chestermiller]

Hey AJ. Don't feel bad. I've had lots of practical experience with solid deformational mechanics. In my judgement, this was not an Introductory Physics problem. Just hang in there.

Chet

 

[mbigras]

From the conditions on the vertical orientation of the wire, you get that

YA = 1000 mg

Let y represent the distance that the center of the wire moves down. Then, from the pythagorean theorem,
\left( \frac{l}{2}\right) ^2=\left( \frac{l_0}{2}\right) ^2+y^2
Solving for l/2:
\left( \frac{l}{2}\right) =\sqrt{\left( \frac{l_0}{2}\right) ^2+y^2}≈\left( \frac{l_0}{2}\right)+\frac{y^2}{l_0}
From this, strain=\frac{l/2-l_0/2}{l_0/2}=2\left(\frac{y}{l_0}\right)^2

Let T represent the tension in the wire. Force balance on hanging weight:
2T\frac{y}{l_0/2}=mg

How is the tension related to Y, A, and the strain in the wire?

Thank you so much for this explanation. Something that comes to mind:
How did you know to make this approximation?
\sqrt{\left( \frac{l_0}{2}\right) ^2+y^2}≈\left( \frac{l_0}{2}\right)+\frac{y^2}{l_0}

 

[Chestermiller]

Thank you so much for this explanation. Something that comes to mind:
How did you know to make this approximation?
\sqrt{\left( \frac{l_0}{2}\right) ^2+y^2}≈\left( \frac{l_0}{2}\right)+\frac{y^2}{l_0}

Hi MBIGRAS. Welcome to Physics Forums.

Answer to your question: From experience with clotheslines, I just knew that y was going to be small compared to l₀/2. So, I just used the binomial expansion (a+b)ⁿ with n = 1/2 and a = (l₀/2)².

Chet