E field inside wires during transient state

[DoobleD]

I've come across an instructive paper which explains qualitatively what happens inside wires of a simple circuit during the transient state, leading to the steady state where there is an uniform E field everywhere inside the wires.

Here are two figures from the paper which are pretty much self explanatory :

What I don't understand is that sentence from figure 6 :

"pile-up of surface charge will continue until the net electric field does point to the left"

Why does the pile up of charges continues even after the net field becomes 0 ? Why charges keep piling up until the E field reverses ? Shouldn't the pile up stops when the net E field reaches 0 ?

 

[Dale]

Why does the pile up of charges continues even after the net field becomes 0 ? Why charges keep piling up until the E field reverses ? Shouldn't the pile up stops when the net E field reaches 0 ?

When the E field at one point reaches zero then, per Ohm's law, the current density at that point is 0. However if the E field is not zero at other points then there will continue to be current at those points which will lead to changes in charge at those points. The E fields from those distant points will continue to change the E field at the point where it is 0, even though there is no current at that point.

 

[DoobleD]

Thanks for answering Dale. Anyway I try it, I think I'm not understanding what you wrote correctly. When I try to imagine the scenario of charges moving, I end up with the net field pointing in the wrong direction. Here is a drawing that tries to explain it :

In the upper drawing, I imagine the net E field of the center wire of the previous figures to be 0. The net field is not 0 on the bends due to the surface charges having piled up. So around the bends, charges move again, but that move make the E field from the capacitor charges win again (lower drawing), with a net field to the right again instead of left.

It's not easy to explain sorry. And I'm sure I misunderstanding things, but can't see what I'm doing wrong.

 

[Dale]

Frankly, I have encountered this paper before and I think their approach is not very good. Actually, I think that it is rather bad. I have run into other people that seemed to think it was helpful for them, but if it causes you ANY confusion then I would recommend dropping it without a second thought.

The reason that I don't like it is that it is only useful if you already know the answer. It provides no method for calculating anything.

 

[DoobleD]

I was glad to find this paper actually, because I always felt the usual circuit initial approach weird. When we study EM theory, we start with charges, E fields, and potential.

Then when we start circuit analysis, we suddenly ignore all about charges and fields, and instead jump to everything about potential. Almost nothing is said about what happens in circuit, why it behaves the way it does.

I found that frustrating and very non intuitive. Charges and force fields are "simpler" notion than potential, more fundamental explanations.

Now I understand why circuit analysis is teach that way. It's much easier to analyze a circuit via potential considerations, and look at the E field or charges distribution only brings useless complexity.

However, it kind of sucks that we just ignore what happens inside the circuit. I personnally need to have at least a qualitative understanding of what's actually happening when I learn about a physical phenomenon. That's basically what motivates me, learn how things work.

That's why I liked the paper. It was almost a relief to see I wasn't the only one to think circuit analysis introductions miss so much deep explanations. However, the paper does bring confusion because it doesn't explain everything.

But it's too late now, I need to understand what happens :D How the E field end up being uniform and along the wires everywhere.

On a side note, I also don't get how, in an idealized wire or a superconductor, charges are able to follow the curves of the wires. No net field inside should imply charges can't turn. There must be E fields inside superconductors, at least at some particular moments maybe. Anyway that's off post.

 

[tech99]

I was glad to find this paper actually, because I always felt the usual circuit initial approach weird. When we study EM theory, we start with charges, E fields, and potential.

Then when we start circuit analysis, we suddenly ignore all about charges and fields, and instead jump to everything about potential. Almost nothing is said about what happens in circuit, why it behaves the way it does.

I found that frustrating and very non intuitive. Charges and force fields are "simpler" notion than potential, more fundamental explanations.

Now I understand why circuit analysis is teach that way. It's much easier to analyze a circuit via potential considerations, and look at the E field or charges distribution only brings useless complexity.

However, it kind of sucks that we just ignore what happens inside the circuit. I personnally need to have at least a qualitative understanding of what's actually happening when I learn about a physical phenomenon. That's basically what motivates me, learn how things work.

That's why I liked the paper. It was almost a relief to see I wasn't the only one to think circuit analysis introductions miss so much deep explanations. However, the paper does bring confusion because it doesn't explain everything.

But it's too late now, I need to understand what happens :D How the E field end up being uniform and along the wires everywhere.

On a side note, I also don't get how, in an idealized wire or a superconductor, charges are able to follow the curves of the wires. No net field inside should imply charges can't turn. There must be E fields inside superconductors, at least at some particular moments maybe. Anyway that's off post.

When the switch is turned on, is it not correct that a wavefront travels along the wire? The magnitude depends only on the voltage and the characteristic impedance of the wire and does not depend on the load resistance. The wavefronts on each wire are of opposite polarity and meet in the load, where some of the energy is absorbed and some reflected. This "RF" method of thinking about the conditions immediately after switch-on seems more realistic.

 

[Dale]

I was glad to find this paper actually, because I always felt the usual circuit initial approach weird. When we study EM theory, we start with charges, E fields, and potential.

Then when we start circuit analysis, we suddenly ignore all about charges and fields, and instead jump to everything about potential. Almost nothing is said about what happens in circuit, why it behaves the way it does.

There ate three theories of electromagnetism. The first is çircuits, the second is Maxwells equations, and the third is QED. I would on the first lecture explain the difference and the assumptions between the theories. Then I would carefully teach only about the subject they are currently studying, and avoid bringing in material from future courses. That would mean that a lot of questions would be answered with, "we won't cover that until ..."

 

[DoobleD]

I would on the first lecture explain the difference and the assumptions between the theories.

That is clearly something I'd like to see in courses. As a student we don't have a clear vision or "big picture" of physics and its different fields. Its getting better everyday though.

 

[DoobleD]

When the switch is turned on, is it not correct that a wavefront travels along the wire? The magnitude depends only on the voltage and the characteristic impedance of the wire and does not depend on the load resistance. The wavefronts on each wire are of opposite polarity and meet in the load, where some of the energy is absorbed and some reflected. This "RF" method of thinking about the conditions immediately after switch-on seems more realistic.

I don't know much about guided waves inside mediums so that doesn't talk much to me yet. However even if that method of thinking works better, it should still be possible to understand why and how the net E field inside a circuit's wire does not go to 0. In terms of (approximate) charge distribution.

 

[Dale]

To give you a feel for the math required to calculate the surface charges, you may want to look at this paper, particularly the beginning portion.

http://depa.fquim.unam.mx/amyd/arch...ia_a_otros_elementos_de_un_circuito_20867.pdf

The scenario calculated there is much simpler than what you are asking because they used a straight wire and only considered the final steady state. The math you are asking for is considerably more difficult.

 

[cnh1995]

I was glad to find this paper actually, because I always felt the usual circuit initial approach weird. When we study EM theory, we start with charges, E fields, and potential.

Then when we start circuit analysis, we suddenly ignore all about charges and fields, and instead jump to everything about potential. Almost nothing is said about what happens in circuit, why it behaves the way it does.

I found that frustrating and very non intuitive. Charges and force fields are "simpler" notion than potential, more fundamental explanations.

Now I understand why circuit analysis is teach that way. It's much easier to analyze a circuit via potential considerations, and look at the E field or charges distribution only brings useless complexity.

However, it kind of sucks that we just ignore what happens inside the circuit. I personnally need to have at least a qualitative understanding of what's actually happening when I learn about a physical phenomenon. That's basically what motivates me, learn how things work.

That's why I liked the paper. It was almost a relief to see I wasn't the only one to think circuit analysis introductions miss so much deep explanations. However, the paper does bring confusion because it doesn't explain everything.

But it's too late now, I need to understand what happens :D How the E field end up being uniform and along the wires everywhere.

On a side note, I also don't get how, in an idealized wire or a superconductor, charges are able to follow the curves of the wires. No net field inside should imply charges can't turn. There must be E fields inside superconductors, at least at some particular moments maybe. Anyway that's off post.

I had exactly the same feeling when I read it a few months ago, after one of my professors suggested me to google 'surface charge feedback in electrical circuits.' It really connects electrostatics and electrical circuits. There are videos on Youtube regarding this example. Also, there is a video "proving" the existence of surface charges across the components in a circuit.

 

[cnh1995]

How the E field end up being uniform and along the wires everywhere.

I believe it happens because of the 'feedback' of the surface charges. During transient, electric field is non-uniform everywhere. That leads to non-uniform currents. That creates a non uniform charge distribution inside the wire. Somewhere, -ve charge is excess, somewhere +ve charge is excess. This excess charge ends up on the surface(basic electrostatics) and forms 'surface charge rings'. These rings continue to form till there are no non-uniform currents (sounds intuitive). That means, this transient stops when the field everywhere in the circuit becomes uniform. The field inside the wire is actually formed by these rings(along their axis). Hence, the field is 'guided' by the wire i.e. it follows the wire regardless of its shape, twists and turns.

 

[tech99]

I believe it happens because of the 'feedback' of the surface charges. During transient, electric field is non-uniform everywhere. That leads to non-uniform currents. That creates a non uniform charge distribution inside the wire. Somewhere, -ve charge is excess, somewhere +ve charge is excess. This excess charge ends up on the surface(basic electrostatics) and forms 'surface charge rings'. These rings continue to form till there are no non-uniform currents (sounds intuitive). That means, this transient stops when the field everywhere in the circuit becomes uniform. The field inside the wire is actually formed by these rings(along their axis). Hence, the field is 'guided' by the wire i.e. it follows the wire regardless of its shape, twists and turns.

I feel that an "RF engineering", or transmission line, approach will give the correct answer, including the skin effect, where the initial current is on the surface, gradually penetrating deeper as the transient dies down, and the guided waves which will travel on the circuit. There will also be radiation, particularly from bends and discontinuities, which an RF engineering approach will in principle correctly describe.

 

[cnh1995]

I feel that an "RF engineering", or transmission line, approach will give the correct answer, including the skin effect, where the initial current is on the surface, gradually penetrating deeper as the transient dies down, and the guided waves which will travel on the circuit. There will also be radiation, particularly from bends and discontinuities, which an RF engineering approach will in principle correctly describe.

I don't know much about RF engineering and waveguide approach. But I found this theory extremely helpful to understand the concept of 'voltage drops' in terms of the surface charge gradient.

 

[jasonRF]

To give you a feel for the math required to calculate the surface charges, you may want to look at this paper, particularly the beginning portion.

http://depa.fquim.unam.mx/amyd/arch...ia_a_otros_elementos_de_un_circuito_20867.pdf

The scenario calculated there is much simpler than what you are asking because they used a straight wire and only considered the final steady state. The math you are asking for is considerably more difficult.

Thanks DaleSpam. That is a nice paper. A few weeks ago I worked out the straight wire problem discussed in that paper and still find the paper enlightening. I worked out the problem on my own as I was particularly interested in the fact that there had to be a radial component of $\mathbf{E}$ outside the wire as energy is transmitted along the wire (Poynting vector outside wire must have component along wire). If you let the wire be in free space with zero potential at infinity, then the result is an ugly sum of modified Bessel functions that yields no insight - that is the version I did first, but plotting the sums and looking at asymptotic approximations made me realize there was a better way.

EDIT: correction: I first solve the problem of a wire down the inside of a finite cylinder (finite in r and z), then saw that the limit of a very long cylinder gave nicer results that were consistent with ain infinitely long cylinder that was only finite in r.

When the switch is turned on, is it not correct that a wavefront travels along the wire? The magnitude depends only on the voltage and the characteristic impedance of the wire and does not depend on the load resistance. The wavefronts on each wire are of opposite polarity and meet in the load, where some of the energy is absorbed and some reflected. This "RF" method of thinking about the conditions immediately after switch-on seems more realistic.

I tend to think of a microwave engineering approach to these problems as well since I tend to think in terms of waves whenever possible. Certainly the transient will not travel faster than the speed of light along the wire, and when it encounters changes in impedance there will be reflections and transmission. However, in this case getting quantitative results is not so easy. Not only do you have a lossy guiding structure, but the geometry makes the equations for the fields fairly difficult.

Jason

 

[tech99]

Thanks DaleSpam. That is a nice paper. A few weeks ago I worked out the straight wire problem discussed in that paper and still find the paper enlightening. I worked out the problem on my own as I was particularly interested in the fact that there had to be a radial component of $\mathbf{E}$ outside the wire as energy is transmitted along the wire (Poynting vector outside wire must have component along wire). If you let the wire be in free space with zero potential at infinity, then the result is an ugly sum of modified Bessel functions that yields no insight - that is the version I did first, but plotting the sums and looking at asymptotic approximations made me realize there was a better way.

EDIT: correction: I first solve the problem of a wire down the inside of a finite cylinder (finite in r and z), then saw that the limit of a very long cylinder gave nicer results that were consistent with ain infinitely long cylinder that was only finite in r. I tend to think of a microwave engineering approach to these problems as well since I tend to think in terms of waves whenever possible. Certainly the transient will not travel faster than the speed of light along the wire, and when it encounters changes in impedance there will be reflections and transmission. However, in this case getting quantitative results is not so easy. Not only do you have a lossy guiding structure, but the geometry makes the equations for the fields fairly difficult.

Jason

Agree with Jason. It also seems to me that in addition to an EM wave being guided along by the wire, a ripple must pass along the electrons, and the two must be in energy equilibrium.

 

[DoobleD]

To give you a feel for the math required to calculate the surface charges, you may want to look at this paper, particularly the beginning portion.

http://depa.fquim.unam.mx/amyd/arch...ia_a_otros_elementos_de_un_circuito_20867.pdf

That paper is awesome, especially to understand the fields outside wires. But it assumes a non zero e field inside wires fromthe begenning, and don't say much about it's formation during the transient state.

The math you are asking for is considerably more difficult.

I'm not looking that much to the maths, I'd be happy with a qualitative explanation.

I had exactly the same feeling when I read it a few months ago, after one of my professors suggested me to google 'surface charge feedback in electrical circuits.' It really connects electrostatics and electrical circuits. There are videos on Youtube regarding this example. Also, there is a video "proving" the existence of surface charges across the components in a circuit.

Good to hear it's a common feeling ! That's right, in case someone is passing by, courses videos and demo from the authors of the paper are available here.

I believe it happens because of the 'feedback' of the surface charges. During transient, electric field is non-uniform everywhere. That leads to non-uniform currents. That creates a non uniform charge distribution inside the wire. Somewhere, -ve charge is excess, somewhere +ve charge is excess. This excess charge ends up on the surface(basic electrostatics) and forms 'surface charge rings'. These rings continue to form till there are no non-uniform currents (sounds intuitive). That means, this transient stops when the field everywhere in the circuit becomes uniform. The field inside the wire is actually formed by these rings(along their axis). Hence, the field is 'guided' by the wire i.e. it follows the wire regardless of its shape, twists and turns.

What you describe is indeed what happens and what is explained in the paper. At steady state, I understand why the rings of charges make a non zero net field inside. Where I'm in trouble is during the process of charges moving, during the transient state : to me, the charges should move in the wires until they have canceled all internal net E field. But in reality, that's not the case. Why ? When you place a charge near a conductor outside of a circuit, the net field inside the conductor vanishes. In the case of a circuit, it does not, whereas the circuit IS a conductor.
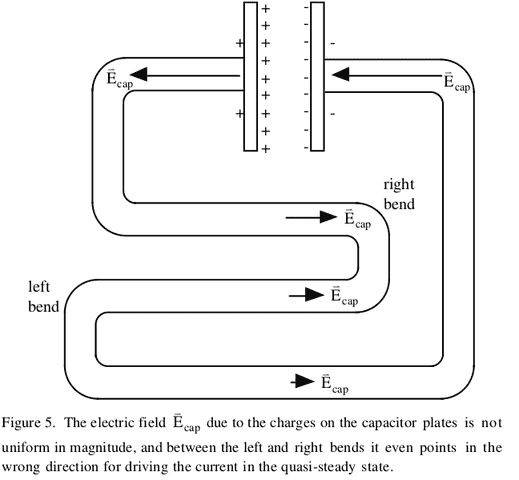
To explain what troubles me precisely, let's say, in the following, that I am an electron located between the left and the right bend, in the circuit drawn on the paper (see figures in the OP). Let's also pretend electrons will move one by one during the transient state.

Here is what happens (we should all agree, I think, from step 1 to 5, then step 6 is my trouble) :

Step 1 (t = 0) : Right now, the net field is only due to the battery charges. Where I am located (between the bends), this net field points to the right. Thus, being an electron, I feel a force to the left. I move to the left bend.

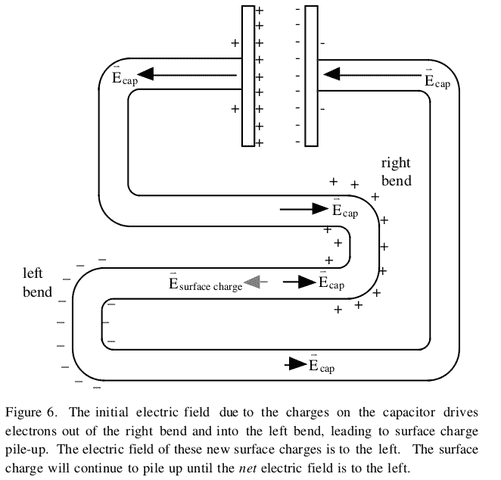
Step 2 : I am now located at the left bend (somewhere at the surface). The left bend is a little bit more negatively charged due to me, and therefore the right bend is a little more positively charged. Thus, I "created" a small field to the left (the polarization field).

That small field of me will add to the field due to the battery charges, making the net field (polarization field + battery field) between the bends diminish in magnitude.

Step 3 : Another electron located between the bends move, as I did. Weakening a little more the net field to the right located between the bends.

Step 4 : As more and more electrons travel to the left, the net field between the bends -which still points to the right- is getting smaller and smaller and smaller in magnitude (because the polarization field -which points to the left- is getting stronger and stronger).

Step 5 : At some instant, there is so much electrons at the left bend, that the polarization field between the bends, which points to the left, is EXACTLY equal in magnitude to the battery field (that field never changed during the whole process). Thus, the net field between the bends now equals 0. At this particular instant, the polarization field and the battery field cancel each other at this "between the bends" location.

I would say so far this agrees with the paper and reality (apart from the fact that many electrons move simultaneously, not one after the other of course).

STEP 6 : Step 6 is my trouble.

Reality says : even more electrons will leave the location between the bends. They will move to the left, making the net field becoming not 0 again, but pointing to the left.

My head says : the net field between the bend is 0 now (from step 5). The electrons should NOT feel any force anymore. They shouldn't move anymore. Everything should stop. Equilibrium has been reached.Somewhere in this process, I must misunderstand something fundamental. Do you see it ?

 

[DoobleD]

I've just re read DaleSpam's initial answer, and got a better understanding of it. This might be it. He wrote :

When the E field at one point reaches zero then, per Ohm's law, the current density at that point is 0. However if the E field is not zero at other points then there will continue to be current at those points which will lead to changes in charge at those points. The E fields from those distant points will continue to change the E field at the point where it is 0, even though there is no current at that point.

Okay, so, let's say I'm at "step 5" (see my previous post). The net field where I am is 0. BUT, as Dale mentioned, there are other places in the circuit where the net field is not 0, charges are still moving there.

Therefore, it seems reasonable to think that the displacement of those charges, located somewhere else in the circuit, will affect the net field at the "between the bends" location (and everywhere else of course). Which solves the "why the net field doesn't end up being 0" question.

So all those little transient disorganised currents everywhere in the circuit continuously affect the net field anywhere, affecting the little currents, and so on and so on. When does this stops ? When the little currents are all synchronized ! Forming one only uniform current. Because only then, the net field is stable everywhere. => Steady state.

This seems to answer my question. Is that it ? Did I correctly understood your answer Dale ?

EDIT : My phrasing is sometimes not correct because I sometimes refer to the net field between the bends being 0 (the so called "step 5" above) while this is not taking in account the contribution from the other charges located somewhere else. Not really a net field. So actually the net (all charges everywhere) field might never reach 0 at any point during the whole process.

 

[cnh1995]

I've just re read DaleSpam's initial answer, and got a better understanding of it. This might be it. He wrote :
Okay, so, let's say I'm at "step 5" (see my previous post). The net field where I am is 0. BUT, as Dale mentioned, there are other places in the circuit where the net field is not 0, charges are still moving there.

Therefore, it seems reasonable to think that the displacement of those charges, located somewhere else in the circuit, will affect the net field at the "between the bends" location (and everywhere else of course). Which solves the "why the net field doesn't end up being 0" question.

So all those little transient disorganised currents everywhere in the circuit continuously affect the net field anywhere, affecting the little currents, and so on and so on. When does this stops ? When the little currents are all synchronized ! Forming one only uniform current. Because only then, the net field is stable everywhere. => Steady state.

This seems to answer my question. Is that it ? Did I correctly understood your answer Dale ?

I Agree..Even if local field is 0, its not 0 everywhere at the same time. So the charges will still be moving and it will stop only when the E field inside is uniform.

 

[Dale]

This seems to answer my question. Is that it ? Did I correctly understood your answer Dale ?

Yes, I believe so. I think that is as much of an answer that can be given without some heavy math.

 

[DoobleD]

Awesome. :D Thank you very much guys for helping.

 

[Dale]

. If you let the wire be in free space with zero potential at infinity, then the result is an ugly sum of modified Bessel functions that yields no insight - that is the version I did first, but plotting the sums and looking at asymptotic approximations made me realize there was a better way.

I just found this paper yesterday. It seems to have a decent insight-driven qualitative method for finding the surface charge distribution.

https://www.tu-braunschweig.de/Medien-DB/ifdn-physik/ajp000782.pdf

In the paper it is entirely focused on the steady state, but the method they use would apply to the transient state also, just with a different set of equipotential lines.

 

[jasonRF]

I just found this paper yesterday. It seems to have a decent insight-driven qualitative method for finding the surface charge distribution.

https://www.tu-braunschweig.de/Medien-DB/ifdn-physik/ajp000782.pdf

In the paper it is entirely focused on the steady state, but the method they use would apply to the transient state also, just with a different set of equipotential lines.

Thanks - that is a beautiful paper. Haven't really read it yet, but the figures are great (I especially like the parallel resistor example in the last figure) and what text I have read is very clear. I'm glad to see it is the American Journal of Physics; hopefully some physics teachers use this to help teach this when appropriate. It would be a great basis for a simple 'project' for those learning EM, both for electrical engineers and physicists.

jason

 

[DoobleD]

I have being simultaneously discussing my issue by mail with the OP paper's authors. The following part of the discussion from Bruce Sherwood might be of interest for people here :


"The following two papers, inspired by our paper and textbook, use the surface charge model to calculate the surface charge distributions on a number of circuit configurations:

Norris W. Preyer, “Surface charges and fields of simple circuits,” Am. J. Phys. 68(11), 1002–1006 (2000).

Norris W. Preyer, “Transient behavior of simple RC circuits,” Am. J. Phys. 70(12), 1187–1193
(2002). In this article Preyer includes retardation effects.

The surface charge distributions found in the program 18-SurfaceCharge found at matterandinteractions.org/student were calculated by using a modified version of Preyer's approach, with higher accuracy and in 3D thanks to advances in computer technology. (You can go directly to the program with tinyurl.com/SurfaceCharge.)

The basic scheme is a relaxation algorithm. Divide the surfaces into small tiles. Start with no charges on these tiles. Calculate the field at the locations of these tiles, due to external charges. Calculate the changes in the charges of the tiles due to these fields. Repeat, now including the fields contributed by the now-charged tiles. Repeat until the charge on one or more representative tiles no longer changes."


"Surface charges and fields of simple circuits" is available here. This one is actually referenced in "Energy flow from a battery to other circuit elements: Role of surface charges".

"Transient behavior of simple RC circuits" is available here (couldn't find a direct PDF link).