etf
- 179
- 2
Here is my task and my attempt of solution:
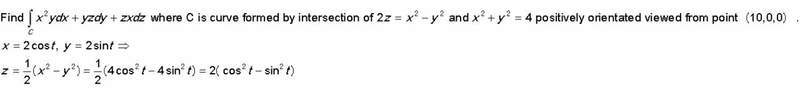
How to use fact that C is positively orientated viewed from point (10,0,0)? I'm not sure I understand it.
How to use fact that C is positively orientated viewed from point (10,0,0)? I'm not sure I understand it.