SansaStark
- 15
- 0
Hello!
I'm struggling with a probably easy physics question concerning random walks. Here I have the slide regarding this:
Delta is the distance that a particle moves.
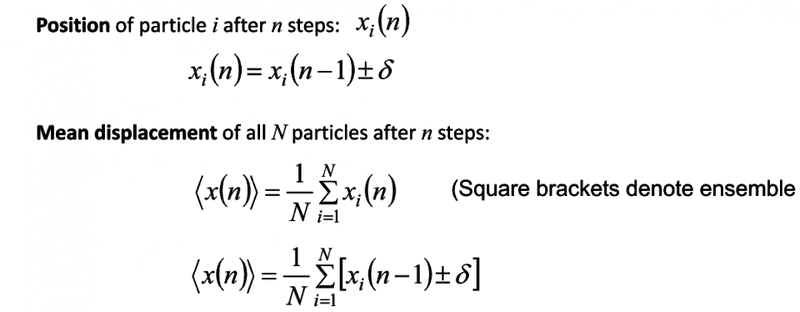
Can someone explain where the n-1 initially comes from? Does it have to do wtih the concept of the degrees of freedom?
Than you already! Regards, Vera
I'm struggling with a probably easy physics question concerning random walks. Here I have the slide regarding this:
Delta is the distance that a particle moves.
Can someone explain where the n-1 initially comes from? Does it have to do wtih the concept of the degrees of freedom?
Than you already! Regards, Vera