karush
Gold Member
MHB
- 3,240
- 5
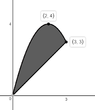
$\textsf{Find the volume of the solid generated by revolving the region
about y-axis.Given the boundares of }\\$
\begin{align*} \displaystyle
y&=4x-x^2\\
y&=x\\
\end{align*}
Ok, I presume since this is rotated around the y-axis that we have to rewrite the equations in terms of y
$y=-(x^2-4x)$
$4-y=(x-2)^2$
$\sqrt{4-y}=x-2$
$\sqrt{4-y}+2=x$
and
$x=y$
But the graph is not complete and is this not the same volume if it were rotated around the x-axis.
I thought this was going to be very easy, but going around the y-axis was confusing.
about y-axis.Given the boundares of }\\$
\begin{align*} \displaystyle
y&=4x-x^2\\
y&=x\\
\end{align*}
Ok, I presume since this is rotated around the y-axis that we have to rewrite the equations in terms of y
$y=-(x^2-4x)$
$4-y=(x-2)^2$
$\sqrt{4-y}=x-2$
$\sqrt{4-y}+2=x$
and
$x=y$
But the graph is not complete and is this not the same volume if it were rotated around the x-axis.
I thought this was going to be very easy, but going around the y-axis was confusing.