Decide volume given two functions

[Nivelo]

Sorry if i made any language errors, english is not my first language.
Question: An area in the first quadrant (x=>0,y=>0) is limited by the axis and the graphs to the functions f(x)=x^2-2 and g(x)=2+x^2/4. When the area rotates around the y-axis a solid is created. Calculate the volume of this solid.

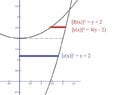
I want to calculate with the disc method. I set h(x)=g(x)-f(x) since g(x)>f(x) in this area. Since x>=0 i check where the lower function crosses the x-axis and get
x^2-2=0 which gives x=sqrt(2) (since x can't be negative). The upper limit is where f(x)=g(x), so
x^2-2=x^2/4+2 which gives x=4/sqrt(3).
One of the discs that i want to sum up should have the volume pi*radius^2*dy.I get the radius from solving x^2 from h(x)=y.And so i get that the volume should be
I=pi/3* integral from 0 to 10/3 of (16-4*y)dy. But its not the right answer and i don't know where i went wrong. Could anyone tell me where i messed up and try to help me solve this one?

Thanks in advance, appreciate all the help!

 

[HallsofIvy]

You are going to have a problem with the "disk method"! From y= -2 to y= 2, your "disks" are entirely bounded by the first function $$y= x^2- 2$$ so, for a given y, the radius is $$x= \sqrt{y+ 2}$$. However, from y= 2 to $$\frac{4}{\sqrt{2}}= 2\sqrt{2}$$ your disk has a "hole" in it because the second parabola, $$y= 2+ \frac{x^2}{4}$$ comes into play. You could use the disk method from y= -2 to y= 2 and then use the "washer method" from y= 2 to $$y= 2\sqrt{2}$$.

But I would recommend, instead, the "cylinder method", using x as the variable, rather than y. For a given x, we have a cylinder with inner radius x, height from $$y= x^2- 2$$ up to $$y= 2+ \frac{x^2}{4}$$ so height is $$2- \frac{x^2}{4}- (x^2- 2)= 4- \frac{5x^2}{4}$$. That is, the circumference is $$2\pi x$$, the surface area is $$2\pi x\left(4- \frac{5x^2}{4}\right)= 2\pi\left(4x- \frac{5x^3}{4}\right)$$ and, with thicknes dx, volume $$2\pi\left(4x- \frac{5x^3}{4}\right)dx$$. Integrate that from x= 0 to $$x= \frac{4\sqrt{3}}{3}$$.​

 

[skeeter]

disks & washers about the y-axis ...

$$V = \pi \int_0^2 (y+2) \, dy + \pi \int_2^{4/\sqrt{3}} (y+2) - 4(y-2) \, dy$$

note ... images should be r(y) for the disks and R(y) & r(y) for the washers

 

[Nivelo]

You are going to have a problem with the "disk method"! From y= -2 to y= 2, your "disks" are entirely bounded by the first function $$y= x^2- 2$$ so, for a given y, the radius is $$x= \sqrt{y+ 2}$$. However, from y= 2 to $$\frac{4}{\sqrt{2}}= 2\sqrt{2}$$ your disk has a "hole" in it because the second parabola, $$y= 2+ \frac{x^2}{4}$$ comes into play. You could use the disk method from y= -2 to y= 2 and then use the "washer method" from y= 2 to $$y= 2\sqrt{2}$$.

But I would recommend, instead, the "cylinder method", using x as the variable, rather than y. For a given x, we have a cylinder with inner radius x, height from $$y= x^2- 2$$ up to $$y= 2+ \frac{x^2}{4}$$ so height is $$2- \frac{x^2}{4}- (x^2- 2)= 4- \frac{5x^2}{4}$$. That is, the circumference is $$2\pi x$$, the surface area is $$2\pi x\left(4- \frac{5x^2}{4}\right)= 2\pi\left(4x- \frac{5x^3}{4}\right)$$ and, with thicknes dx, volume $$2\pi\left(4x- \frac{5x^3}{4}\right)dx$$. Integrate that from x= 0 to $$x= \frac{4\sqrt{3}}{3}$$.​

Thanks for the response, i solved it. Since one of the demands was that y>=0 i broke the solid down into two parts, one from x=0 to x=sqrt(2) which is before the lower function crossed the x-axis f(x)=0. The other part was from where the lower function crosses the x-axis f(x)=0 to where the upper and lower function crosses f(x=g(x) ,which gives x=4/sqrt(3). From x=0 to x=sqrt(2) the height of one "rectangle" is the distance from the upper function to the y-axis and from x=sqrt(2) to x=4/sqrt(3) the height is the difference g(x)-f(x).
Volume = (2*pi*integral from 0 to sqrt(2) of g(x)) + (2*pi*integral from sqrt(2) to 4/sqrt(3) of g(x)-f(x)) = 52*pi/6