Solmyros
- 21
- 0
- TL;DR
- Boundary conditions give different result depending on whether the quantum well is defined from 0 to L or from -L/2 to +L/2.
Greetings everyone,
Exactly as the title says. I am reaching to something strange and I do not know what I am missing. It must be something obvious...
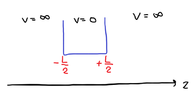
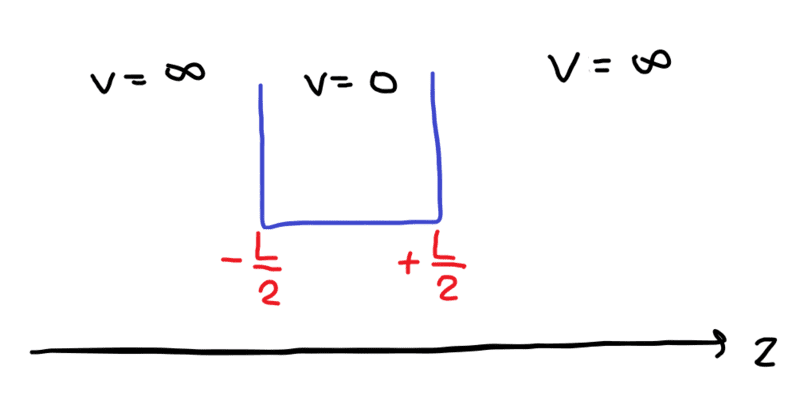
case 1: -L/2 to L/2
After taking the Schrödinger equation and considering potential equal to zero inside we reach at this: $$Ψ=A×e^{ikz}+B×e^{- ikz}$$
Boundary conditions
Outside the well the potential is assumed infinite, so the wavefunction is equal to zero:
Substituting (3) in 2. we get: $$k=\frac{n \times \pi}{L}, where \ n=0,1,2,... (4)$$
Therefore from (3) we get: $$B=−A \times e^{−inπ}$$
And finally, if $$n=2m, where \ m=0,1,2,...$$ we get from the original Schrödinger Equation: $$\Psi_{even}(z) = A \times ( e^{i k z} - e^{- i k z)} = 2 i A \sin{(kz)} \ (5)$$
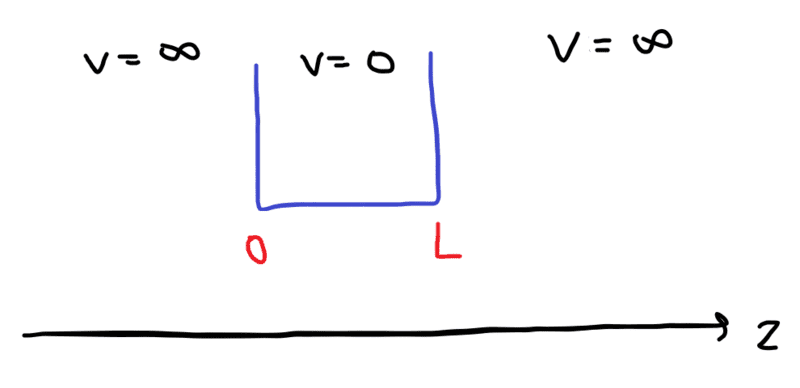
case 2: 0 to L
After taking the Schrödinger equation and considering potential equal to zero inside we reach at this: $$Ψ=A'×e^{ikz}+B'×e^{- ikz}$$
Boundary conditions
Outside the well the potential is assumed infinite, so the wavefunction is equal to zero:
So, we get from the original Schrödinger Equation: $$\Psi(z) = A' \times ( e^{i k z} - e^{- i k z)} = A' \sin{kz} \ (9)$$
and
$$Ψ(L)=0 = A' \sin{kL} \ which \ gives \ k=\frac{n \times \pi}{L} \ (10), where \ n=0,1,2,... (\ like \ before)$$
But, now if $$n=2m, where \ m=0,1,2,...$$ we get $$\Psi_{even}(z) = A' \sin({\frac {2m \pi }{L}z}) \ (11)$$
Normalization will eventually give the same amplitude, BUT, on the first case the wavefunction is imaginary. This added 'i' is what buffles me.
Thank you in advance for your help.
Exactly as the title says. I am reaching to something strange and I do not know what I am missing. It must be something obvious...
case 1: -L/2 to L/2
After taking the Schrödinger equation and considering potential equal to zero inside we reach at this: $$Ψ=A×e^{ikz}+B×e^{- ikz}$$
Boundary conditions
Outside the well the potential is assumed infinite, so the wavefunction is equal to zero:
- $$\Psi = 0, when \left|{z}\right|>\frac{L}{2}$$
- $$Ψ(−\frac{L}{2})=0 \ (1)$$
- $$Ψ(+\frac{L}{2})=0 \ (2)$$
Substituting (3) in 2. we get: $$k=\frac{n \times \pi}{L}, where \ n=0,1,2,... (4)$$
Therefore from (3) we get: $$B=−A \times e^{−inπ}$$
And finally, if $$n=2m, where \ m=0,1,2,...$$ we get from the original Schrödinger Equation: $$\Psi_{even}(z) = A \times ( e^{i k z} - e^{- i k z)} = 2 i A \sin{(kz)} \ (5)$$
case 2: 0 to L
After taking the Schrödinger equation and considering potential equal to zero inside we reach at this: $$Ψ=A'×e^{ikz}+B'×e^{- ikz}$$
Boundary conditions
Outside the well the potential is assumed infinite, so the wavefunction is equal to zero:
- $$\Psi = 0, \ when \ z \le 0 \ or \ z \ge L$$
- $$Ψ(0)=0 \ (6)$$
- $$Ψ(L)=0 \ (7)$$
So, we get from the original Schrödinger Equation: $$\Psi(z) = A' \times ( e^{i k z} - e^{- i k z)} = A' \sin{kz} \ (9)$$
and
$$Ψ(L)=0 = A' \sin{kL} \ which \ gives \ k=\frac{n \times \pi}{L} \ (10), where \ n=0,1,2,... (\ like \ before)$$
But, now if $$n=2m, where \ m=0,1,2,...$$ we get $$\Psi_{even}(z) = A' \sin({\frac {2m \pi }{L}z}) \ (11)$$
Normalization will eventually give the same amplitude, BUT, on the first case the wavefunction is imaginary. This added 'i' is what buffles me.
Thank you in advance for your help.