1PI one-loop diagrams for phi^3

[ChrisVer]

I wanted to ask, about the $6$-dimensional $\phi ^3$ theory...
The Lagrangian is:
$$ L = \frac{1}{2} (\partial \phi)^2 - c \phi - \frac{m^2}{2} \phi^2 + \frac{g}{3!} \phi^3$$

When I want to draw all the 1-loop 1PI diagrams, should I make something like these:

?

 

[Einj]

In general yes. The \phi^3 theory admits 3-particle vertices. However, it always depends on what kind of correction you want to compute. For example, if you are interested in the propagator (2-point function) then you will consider the diagram a. If you are interested in a 3-particle interaction you will consider b and so on.

P.S. Are you sure about that linear term in \phi it's quite unusual. Also you should be aware that the \phi^3 is an unstable theory when quantized since the energy is unbounded from below.

 

[ChrisVer]

that's why they inserted the linear term, so that there will be a metastable state at some point, which allows to treat the theory perturbatively.

 

[Einj]

Interesting... how would it contribute to the Feynman diagrams? A tadpole?

 

[ChrisVer]

I don;t think it would contribute to Feynman diagram... :(

 

[Einj]

Well it can definitely generate a 1-point function. I'm wordering what does that mean...

 

[ChrisVer]

From the EoM however, it seems there is not to be such a thing...It's like everywhere there is a constant $c$

[ \partial^2 + m^2 ] \phi = c + \frac{g}{2} \phi^2

 

[Orodruin]

If there is a linear term you are not expanding the theory around the metastable point ...

 

[ChrisVer]

Well I am not sure, I'm using what I read in the exercise I was trying to work on...

 

[Einj]

Well the presence of the constant c is not a big deal. Take for example the EOM you wrote before. For small constant \langle\phi\rangle then you can neglect both the box and the \phi^2 and you obtain: \langle\phi\rangle=c, i.e. you field has a non-zero VEV. This is not a problem at all. In particular, it is exactly what happens for example in the Serot-Walechka model for nuclear interactions.

What I was wondering is what is the role of a linear term in the various n-point functions.

 

[ChrisVer]

What I was wondering is what is the role of a linear term in the various n-point functions.

The constant $c$ can play the role of a constant-everywhere existing current with which the field interacts with, as for example in a term \phi \partial_\mu J^\mu?

To get the n-point function (if there exists such a thing) I think you have to start acting on the generating functional with functional derivatives wrt to the current J?

 

[Einj]

Yes, I think you are right. You might need to start inserting a certain number of external currents that then couple to the $\phi$ field.

 

[vanhees71]

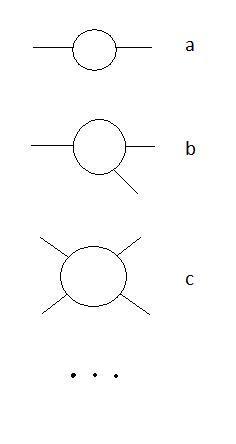
Well, $\phi^3$ theory, is just a playground to learn renormalization techniques (usually in 1+5 dimensional space time in order to have a renormalizable and not a superrenormalizable model). It's not a nice physical theory, because the Hamiltonian is not bounded from below and thus there's no ground state for the interacting theory. The linear term in the Lagrangian is needed to get rid of tadpole diagrams. This trouble you don't have with $\phi^4$ theory (in 1+3 dimensions). I don't see, why one should use $\phi^3$ theory instead of $\phi^4$ theory when introducing renormalization techniques. Perhaps it's done in some textbooks (like Collins, Renormalization and Srednicky QFT), because it bears some similarity with spinor QED, where you also only have a three-legged vertex at tree-level.

 

[Einj]

Not necessarily. If you study nuclear matter, i.e. QFT not in vacuum, it turns out that in order to obtain the right equilibrium radius for the nucleons inside a nucleus you need odd powers of your fields. So, yes, in general the $\phi^3$ is an easy playground but it also has some practical use.

 

[vanhees71]

Sure, but for a physical model you should have a Hamiltonian bounded from below, i.e., there should be a ground state. Thus in general you have odd and even powers. For a Dyson-renormalizable model you have powers up to four with the coupling in front of $\phi^4$ positive.

 

[ChrisVer]

Well you of course get $\phi^3$ interactions in more than just "nuclear". cubic terms can appear when introducing for light quarks the Nambu Goto fields [pions and eta]