2.3.361 AP Calculus Exam of differentials of sin wave

In summary, the conversation discusses the difficulty in duplicating a sin wave on Desmos and the possibility of using observation to determine if a graph is a trig function or a polynomial function of degree 3. The importance of the graph's transformations is also mentioned, along with the use of derivatives to make a correct choice.
  • #1
karush
Gold Member
MHB
3,269
5
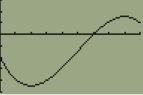
View attachment 9451

image due to graph, I tried to duplicate this sin wave on desmos but was not able to.

so with sin and cos it just switches to back and forth for the derivatives so thot a this could be done just by observation but doesn't the graph move by the transformations

well anyway?
 

Attachments

  • Capture.PNG
    Capture.PNG
    7 KB · Views: 97
Physics news on Phys.org
  • #2
what makes you think it's a trig function ? ... could it also be a polynomial function of degree 3 ? note my calc screenshotas you stated, you don't need the equation of the curve to make the correct choice ...

$\displaystyle h(6) = \int_0^6 f(t) \, dt < 0$

$h'(6) = f(6) = 0$

$h''(6) = f'(6) > 0$
 

Attachments

  • cubic_f.png
    cubic_f.png
    367 bytes · Views: 86

FAQ: 2.3.361 AP Calculus Exam of differentials of sin wave

What is the purpose of the "2.3.361 AP Calculus Exam of differentials of sin wave"?

The purpose of the "2.3.361 AP Calculus Exam of differentials of sin wave" is to assess a student's understanding and application of differential calculus concepts, specifically in relation to the sine function.

What topics are covered in the "2.3.361 AP Calculus Exam of differentials of sin wave"?

The exam covers topics such as derivatives, differentials, and the application of these concepts to the sine function. Students may also be tested on their ability to solve related rates problems involving the sine function.

Is the "2.3.361 AP Calculus Exam of differentials of sin wave" a standardized test?

Yes, the "2.3.361 AP Calculus Exam of differentials of sin wave" is a standardized test developed and administered by the College Board. It is used to determine a student's readiness for college-level calculus courses.

How long is the "2.3.361 AP Calculus Exam of differentials of sin wave"?

The exam is typically 3 hours and 15 minutes long and consists of two sections: a multiple-choice section and a free-response section. The multiple-choice section is 1 hour and 45 minutes long, and the free-response section is 1 hour and 30 minutes long.

What resources are allowed during the "2.3.361 AP Calculus Exam of differentials of sin wave"?

Students are allowed to use a graphing calculator during the exam. However, they are not permitted to use any notes, textbooks, or other resources. All necessary formulas and equations will be provided in the exam booklet.

Similar threads

MHB 9.1.317 AP calculus exam multiple choice derivatives of sin wave
Replies
1
Views
1K
MHB 2.1.314 AP Calculus Exam a particle moves along the x-axis......
Replies
1
Views
1K
MHB 1.4.203 AP calculus practice question on Limits
Replies
1
Views
1K
MHB 1.4.293 AP Calculus Exam a(t) and v(t) t=8
Replies
6
Views
2K
MHB 3.4.238 AP calculus exam Limits with ln
Replies
1
Views
1K
MHB What Is the Total Distance Traveled by the Particle from t = 0 to t = 3?
Replies
4
Views
2K
MHB 4.2.204 AP calculus practice question
Replies
6
Views
2K
MHB 215 AP Calculus Exam Problem Power Rule
Replies
7
Views
2K
MHB 5.1.313 AP Calculus Exam DE on bird weight
Replies
6
Views
1K
MHB 4.1.237 AP calculus exam find area
Replies
4
Views
2K

Hot Threads

Recent Insights

Back
Top