feynman1
- 435
- 29
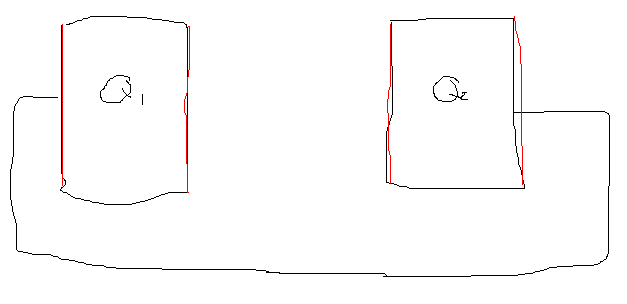
2 separate big conductors initially charged Q1 and Q2. Then connect them with an ideal wire (no resistance). The charges Q1 and Q2 will go to the 4 surfaces (marked red). All the 4 surfaces have an area A. Suppose the 2 conductors form an ideal parallel plate capacitor. How to determine the charges on the 4 red surfaces?