2 Masses connected to a spring

[NTesla]

You have done the calculation so know that $l$ is constant. So your $l$=$x_2-x_1$ means spring between block 1 and block 2 does not change its length like a rod, though the equation is that of harmonic oscillation. Do I catch you right ?

I'm trying to understand your calculation in post #4. You have taken $x_1,x_2$ as coordinates.
$l$ is the length of string at any instant of time. It is not a constant. $l$ changes wrt time.
$l$=$x_2-x_1$, considering that $x_1, x_2$ are coordinates of the masses $m_1$ and $m_2$.
But, the value of $x_2-x_1-l=0$ always.

 

[anuttarasammyak]

Hi. My l is

$$l-l_0=\frac{F_2/m_2-F_1/m_1}{\omega^2}$$

Your l is

It is not a constant. $l$ changes wrt time.
$l$=$x_2-x_1$, considering that $x_1, x_2$ are coordinates of the masses $m_1$ and $m_2$.
But, the value of $x_2-x_1-l=0$ always.

So the equation is written as
$$\ddot{(l_{yours}-l_{mine})}+\omega^2(l_{yours}-l_{mine})=0$$
where
$$\omega^2=k(1/m_1+1/m_2)$$
$$l_{mine}=l_0+\frac{F_2/m_2-F_1/m_1}{\omega^2}$$, constant, and
$$l_{yours}=x_2-x_1=l_{yours}(t)$$ function of time.

$l_{yours}-l_{mine}$ is elongation of spring not from its natural length $l_0$ but from $l_{mine}$ which is interpreted as altered natural length under external constant forces.

 

[haruspex]

@haruspex ,
I've tried to find a relation between CoM's displacement and $x_1$ and $x_2$, but it appears more difficult than I assumed it to be. Here's my work: View attachment 273350

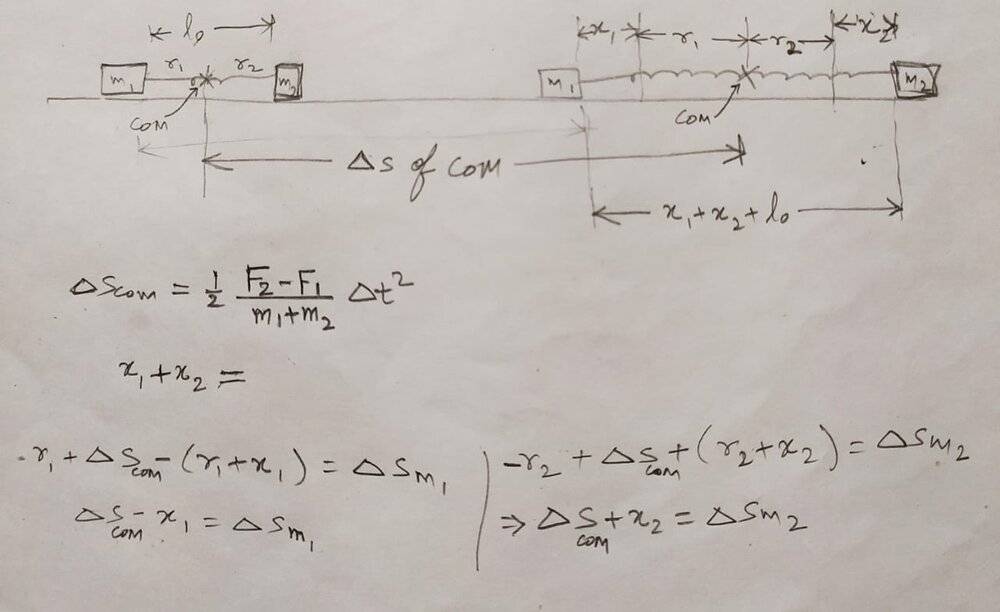
I am not able to figure out the relation. let me know how to proceed.

If m₁ moves x₁ to the left and m₂ moves x₂ to the right then that shifts the "mass moment" m₂ x₂ - m₁ x₁ to the right, so (m₁+m₂)Δs = m₂ x₂ - m₁ x₁, where Δs is positive to the right.

 

[NTesla]

@haruspex, Thank you so much. That was very helpful.

Just one question: If we do not resort to center of mass FoR, and work solely in Ground FoR, then how can we explain that the maximum elongation will happen when both the masses have same velocity as that of velocity of com ?

 

[haruspex]

@haruspex, Thank you so much. That was very helpful.

Just one question: If we do not resort to center of mass FoR, and work solely in Ground FoR, then how can we explain that the maximum elongation will happen when both the masses have same velocity as that of velocity of com ?

Not sure if that's what you meant. There's no problem explaining that; do you mean, how do we use it?
Isn't it the same as saying the two masses have the same velocity?

 

[NTesla]

@haruspex,
When working in CoM FoR, both the masses will seem to be moving in opposite direction and maximum extension in spring will happen when velocity of both the masses is equal to zero at the same instant.

However, when working in Ground FoR, the bodies might seem to be moving in same direction, but maximum extension of spring will happen when both the masses have same speed in same direction. Will it be right to say so.? If yes, then is there an intuitive way to explain that this is the only way possible for string to have maximum elongation in Ground FoR ?

 

[anuttarasammyak]

Hi.

If yes, then is there an intuitive way to explain that this is the only way possible for string to have maximum elongation in Ground FoR ?

At extreme points
$$\dot{l_{yours}}=0$$
It means
$$\dot{x_1}=\dot{x_2}$$
When it is maximum extension
$$\ddot{l_{yours}}=-\omega^2(l_{yours}-l_{mine})< 0$$
For minimum shrink
$$\ddot{l_{yours}}=-\omega^2(l_{yours}-l_{mine})> 0$$

 

[haruspex]

@haruspex,
When working in CoM FoR, both the masses will seem to be moving in opposite direction and maximum extension in spring will happen when velocity of both the masses is equal to zero at the same instant.

However, when working in Ground FoR, the bodies might seem to be moving in same direction, but maximum extension of spring will happen when both the masses have same speed in same direction. Will it be right to say so.? If yes, then is there an intuitive way to explain that this is the only way possible for string to have maximum elongation in Ground FoR ?

If the two masses have different velocities in the ground frame then they are either getting closer or further apart. If closer, they must have been further apart earlier; if further apart, they will be at max separation later. So when at max, the relative velocity must be zero.

 

[NTesla]

@anuttarasammyak and @haruspex : Thank you so much. Your contribution was very helpful and is very much appreciated.