Homework Help Overview
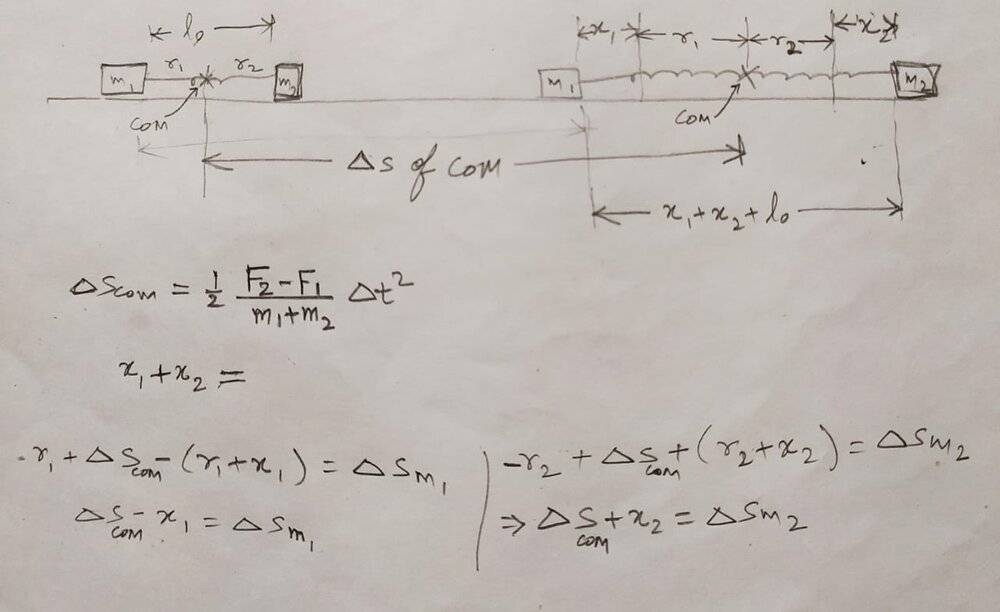
The discussion revolves around solving a problem involving two masses connected by a spring, specifically in the context of a ground frame of reference. Participants explore the dynamics of the system, including forces, accelerations, and oscillatory motion, while contrasting approaches taken in different frames of reference.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning, Assumption checking
Approaches and Questions Raised
- Participants discuss various methods to approach the problem, including energy conservation in different frames, the application of Newton's second law, and the implications of forces acting on the masses. Questions arise about the nature of motion (simple harmonic vs. static) based on how forces are applied.
Discussion Status
The discussion is active, with participants sharing their attempts and reasoning. Some provide insights into the equations of motion and energy considerations, while others express uncertainty about the correct approach in the ground frame. There is no explicit consensus, but various lines of reasoning are being explored.
Contextual Notes
Participants note constraints such as the assumption of starting conditions, the nature of force application (sudden vs. gradual), and the implications for the system's behavior. The complexity of the problem is acknowledged, particularly regarding the coupling of equations and the potential for oscillatory motion.