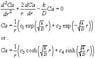2nd order differential equation in Reaction Engineering

[FaNgS]

There's a catalyst pellet in a reactor and I'm supposed to prove an equation for the maximum temperature which is:

Tmax=Ts +[(-H)*(D*Cas)]/k

First thing I did was develop an Energy Balance across the spherical catalyst and I got the following equation:

(1/r^2)*d/dr(r^2*k*dT/dr) + (-H)*(-Rxn) = 0

expanding i get:

d^2T/dr^2 + (2/r)*dT/dr + (-H)*(-Rxn)/k = 0

Boundary Conditions: at r=0, dT/dr =0 AND at r=R, T=Ts (at the catalyst surface i.e. r=R the temperature T = Ts (catalyst surface temperature))

Using the boundary conditions and integrating factor I got
T=Ts + [(-H)(-Rxn)*(R^2-r^2)]/(6*k) ...(eqn 1)

Now for the mole balance across the catalyst I got (where Ca is the concentration):

d^2Ca/dr^2 + (2/r)*dCa/dr - (k/D)*Ca =0 ... (eqn 2)

Boundary Condition: at r=R, Ca=Cas

Can someone confirm the equation I got for temperature (eqn 1) and also for the concentration (eqn 2) how do I go about to solve it??

I tried another way to solve it, as suggested by my instructor, which is by using the un-expanded forms of the energy and mole balance equations which are:

(1/r^2)*d/dr(r^2*k*dT/dr) + (-H)*(-Rxn) = 0

(1/r^2)*d/dr(r^2*D*dCa/dr) + (Rxn) = 0

So here I have the "Rxn" term common in both equations and I combined and got the following after some simplifications:

d^2Ca/dr^2 + 2*dCa/dr = [k/(H*D)]* { r*d^2T/dr^2 + 2*dT/dr}

But in this case it looks way more complicated and I'm not sure how to deal with this type of an equation, since I have 2 derivates on both sides of the equation one with respect to the Concentration Ca and one with respect to temperature T.

not sure which way to proceed and how to proceed

 

[JJacquelin]

Let Ca(r)=(1/r)exp(f(r)) :