SUMMARY
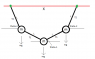
This discussion focuses on solving the angles formed by three equal mass balls (M) connected by massless strings of length (L) in a configuration where two balls are suspended from the ceiling and one is in the middle. The key relationships derived include T1*cos(theta1) = T2*cos(theta2) for the horizontal tension components and the vertical force balance equations T2*sin(theta2) = mg + T1*sin(theta1) and 2*T1*sin(theta1) = mg. The final expressions for the angles are theta2 = arctan(3*tan(theta1)) and X = 2*L*[cos(theta1) + cos(theta2)], indicating a complex relationship that may require numerical methods for specific values of X/L.
PREREQUISITES
- Understanding of basic physics concepts such as tension and equilibrium.
- Familiarity with trigonometric functions and their applications in physics.
- Knowledge of algebraic manipulation and solving equations.
- Experience with numerical methods for solving complex equations.
NEXT STEPS
- Explore the principles of static equilibrium in multi-body systems.
- Learn about numerical methods for solving nonlinear equations.
- Study trigonometric identities and their applications in physics problems.
- Investigate the use of simulation tools for modeling physical systems with constraints.
USEFUL FOR
Physics students, mechanical engineers, and anyone interested in solving complex tension and equilibrium problems in multi-body systems.