8.01 MIT OCW PS1.4: Throw and Catch (Kinematics)

[giodude]

Homework Statement

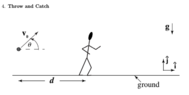
A ball is thrown over the head of a person who is standing a horizontal distance d from the point where the ball was thrown. The initial ball's velocity is at an angle theta with respect to the groun and has a magnitude v0. As soon as the ball is thrown, the person runs with a time-varying acceleration whose component along the x-axis is given by Bt, where B is a positive constant. The person catches the ball at exactly the same height it was thrown from. Assume that the air resistance is negligible and that the gravitational acceleration is directed downward and has magnitude g. Find the constant B.
Express your answer in terms of some or all of the given variables. Use theta, g, d, and v0 as needed.

Relevant Equations

xp0 = d, vp0 = 0, ap0 = 0
xp(t) = d + (1/6)*B*(t^3)
vp(t) = B*(t^2)/2
ap(t) = B*t

xb0 = 0, vb0 = v0, ab0 = 0
xb(t) = v0*cos(theta)*t
vb(t) = v0*cos(theta)
ab(t) = 0

1) Using "The person catches the ball at exactly the same height it was thrown from.", we can isolate t by solving yb(t) = v0*sin(theta)*t - (1/2)*g*(t^2) = 0:
yb(t) = v0*sin(theta)*t - (1/2)*g*(t^2) = 0
v0*sin(theta)*t = (1/2)*g*(t^2)
2*v0*sin(theta) = g*t
t = 2*v0*sin(theta) / g

2) At the time of the catch, the person and the ball have the same x coordinate so we can set xp(t) = xb(t) and plug in t
d + (1/6)*B*(t^3) = v0*cos(theta)*t
B*(t^3) = 6*v0*cos(theta)*t - 6*d
B = (6*v0*cos(theta)*t - 6*d) / (t^3)
B = (6*v0*cos(theta)*t - 6*d) / (2*v0*sin(theta) / g)^3

I believe this is the correct answer. My purpose for posting this here is two fold; to see if I've done it correctly and to try and understand how to physically interpret this outcome so that it intuitively makes sense as well. One way I was thinking about physically interpreting it was through dimensional analysis and checking that there are no lingering dimensions. However, am curious about other modes of approach.

 

[hutchphd]

If you wish somebody to take the time to check your work you need to use LaTex for the equations. Yes there is a learning curve. See "LaTeX Guide below

 

[giodude]

Will do.

 

[haruspex]

B = (6*v0*cos(theta)*t - 6*d) / (2*v0*sin(theta) / g)^3

I believe this is the correct answer.

It is not, quite, an answer to the question posed because you still have a t in there.
Did you check the dimensions? Looks ok to me.
Often, a useful sanity check is a special case for which the answer is obvious, but I don't see such an option here. One special case would be d=0, but the answer is still not obvious for that. $d=v_0\cos(\theta)t$ works, but is too trivial.

 

[giodude]

It is not, quite, an answer to the question posed because you still have a t in there.
Did you check the dimensions? Looks ok to me.
Often, a useful sanity check is a special case for which the answer is obvious, but I don't see such an option here. One special case would be d=0, but the answer is still not obvious for that. $d=v_0\cos(\theta)t$ works, but is too trivial.

Oh, yes! It looks like I forgot to convert that value.

Dimensions seem to properly cancel out. Thanks!