9.1.317 AP calculus exam multiple choice derivatives of sin wave

In summary, the 9.1.317 AP calculus exam consists of multiple choice questions that test students' understanding of derivatives of a sin wave. There are typically around 10-15 questions on derivatives of sin waves, and some common types of questions include finding the derivative at a specific point, finding the average rate of change over an interval, and finding the equation of the tangent line at a given point on the sin wave graph. To prepare for the exam, students should review the concepts of derivatives, particularly those related to sin waves, and practice solving various types of derivative questions. There are also many resources available, such as review books, online practice tests and quizzes, tutoring services, and reviewing class notes and textbook materials.
  • #1
karush
Gold Member
MHB
3,269
5
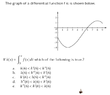
View attachment 9358
ok just posted an image due to macros in the overleaf doc

this of course looks like a sin or cos wave and flips back and forth by taking derivatives
looks like a period of 12 and an amplitude of 3 so...
but to start I was not able to duplicate this on desmos

altho I think by observation alone I think which choices represent the graph.
 

Attachments

  • Capture.PNG
    Capture.PNG
    11 KB · Views: 95
Physics news on Phys.org
  • #2
typo in the accumulation function. should be ...

\(\displaystyle h(x) = \int_0^x f({\color{red}t}) \, dt\)$h'(x) = f(x) \implies h''(x) = f'(x)$$h(6) < 0$ ... why?

$h'(6) = f(6) = 0$

$h''(6) = f'(6) > 0$ ... why?
 

FAQ: 9.1.317 AP calculus exam multiple choice derivatives of sin wave

What is the purpose of the 9.1.317 AP calculus exam multiple choice derivatives of sin wave?

The purpose of this exam is to test students' understanding and application of the derivative of a sine wave, which is a fundamental concept in calculus. It assesses their ability to calculate derivatives of sine functions, as well as their understanding of the properties and applications of these derivatives.

What topics are covered in the 9.1.317 AP calculus exam multiple choice derivatives of sin wave?

The exam covers topics such as the definition of a derivative, the derivative of a sine function, the chain rule, the product and quotient rules, and applications of the derivative to real-world problems. It also includes multiple choice questions that require students to analyze graphs and apply their knowledge of derivatives to solve problems.

How can I prepare for the 9.1.317 AP calculus exam multiple choice derivatives of sin wave?

To prepare for this exam, it is important to review the fundamental concepts of derivatives, particularly those related to the sine function. Practice problems and past exams can also be helpful in familiarizing yourself with the format and types of questions that may be asked. It is also important to have a strong understanding of the properties and rules of derivatives, as well as their applications.

What is the format of the 9.1.317 AP calculus exam multiple choice derivatives of sin wave?

The exam consists of multiple choice questions, with each question having four answer choices. It is typically timed and may include a mix of conceptual and computational questions. The exam is designed to test both the understanding of concepts and the ability to apply them to solve problems.

How is the 9.1.317 AP calculus exam multiple choice derivatives of sin wave scored?

The exam is scored on a scale of 1-5, with 5 being the highest score. The score is based on the total number of correct answers, with no penalty for incorrect answers. A score of 3 or higher is considered passing and may earn college credit, depending on the policies of the individual college or university.

Similar threads

MHB 2.3.361 AP Calculus Exam of differentials of sin wave
Replies
1
Views
1K
MHB 2.1.314 AP Calculus Exam a particle moves along the x-axis......
Replies
1
Views
1K
MHB 215 AP Calculus Exam Problem Power Rule
Replies
7
Views
2K
MHB What Is the Total Distance Traveled by the Particle from t = 0 to t = 3?
Replies
4
Views
2K
Testing Improve Speed for AP Calculus Exam | High School Student
Replies
7
Views
1K
Old AP Physics C Exams: Finding Multiple Choice Sections
Replies
2
Views
3K
Calculus Readiness Multiple Choice Test Answer Key Wrong?
Replies
12
Views
10K
Are These Physics Multiple Choice Answers Correct?
Replies
5
Views
3K
Maximizing Your Scores: Final Exam Help for Multiple Choice and Essay Questions!
Replies
3
Views
9K
End Model Behaviors: Disagreement Between Teacher & Student
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top