karush
Gold Member
MHB
- 3,240
- 5
View attachment 9322
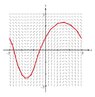
I'm just going to post this image now since my tablet won't render the latex. This is a free response question..
But my experience is that the methods of solving are more focused here at mhb saving many error prone steps..
Mahalo ahead...
I'm just going to post this image now since my tablet won't render the latex. This is a free response question..
But my experience is that the methods of solving are more focused here at mhb saving many error prone steps..
Mahalo ahead...