A. 2 circles that have the same center have their radiuses

[Britney2]

A. 2 circles that have the same center have their radiuses respectively 5 nd 3 cm. From A which is a point of the big circle are constructet the tangents with the small circles and we mark the pint of tangent A and B. Let's mark D and E the points where these tangents touch the big circle. Find the distance of the center O from DE. (my answer is 1.4 cm but i just don't know if I am right)
B. f(x)= (1-x)^1/2 / x Find the limit when x goes to - infinity.

Thanks in advance!

 

[SonyAD]

1.5 cm + 1 cm = 2.5 cm. This is the length of the radius of the outer circle that passes through A. This is the hypotenuse of a right angled triangle.

1.5 cm is the radius of the inner circle which falls perpendicularly on the tangent that comes from A, which is one of the catheti of this triangle.

By Pitagora's Theorem, the other cathetus (half the length of the tangent) is 2 cm. It should be evident that the tangent touches the smaller circle with its exact middle since the circles are concentric. As such, the length of either tangent is 4 cm. This will be important later on.

Now, because this is a right angle triangle we have here, if we draw the height of the tangent point from the hypotenuse, we will obtain two constituent triangles similar to our original triangle but smaller in size.

We need this height and we can compute its length like this
\frac{2}{2.5} \cdot 1.5 cm = 1.2 cm

Ok. Now remember the tangents touch the inner circle at their middle. So we need to scale the height we just calculated by 2 to find half the length of [DE].

So let F be A's projection on [DE]. F will be right at the middle of [DE].

So the distances between D and F and F and E are equal and equate to 2.4 cm. We already know that the distances between D or E and the centre of the two triangles is 2.5. So, by Pitagora's Theorem, let us compute the height of this centre above [DE] out to be 0.7 cm.

 

[zgozvrm]

A. 2 circles that have the same center have their radiuses respectively 5 nd 3 cm. From A which is a point of the big circle are constructet the tangents with the small circles and we mark the pint of tangent A and B. Let's mark D and E the points where these tangents touch the big circle. Find the distance of the center O from DE. (my answer is 1.4 cm but i just don't know if I am right)
B. f(x)= (1-x)^1/2 / x Find the limit when x goes to - infinity.

Thanks in advance!

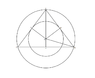
Your problem is not stated very clearly. I'm assuming that you are starting from a point X on the big circle and constructing the 2 tangents to the small circle through point X. (See attached diagram). Then, the tangent points are labeled A and B. The points where the tangent lines cross the large circle are labeled C and D so that you have 2 chords to the big circle, XC and XD, both tangent to the small circle at points A and B, respectively.

If this is correct, I get 1.4cm also:

OX = 5cm since it is a radius to the large circle
OA = 3cm since it is a radius to the small circle
OA must be perpendicular to CX since CX is tangent to the small circle
Also, OB is perpendicular to DX for the same reason
Therefore, triangle OAX makes a right triangle with angle A being the right angle
And triangle OBX is a right triangle with angle B as the right angle
That makes AX = 4cm by Pythagorean theorem
Which means that AC, AX, BD and BX are all equal to 4cm, making CX and DX equal to 8cm

Extend XO until it intersects with CD at a point F
We know that XF must be perpendicular to CD:
triangle OAC = triangle OBD by SAS
Points O and X lie on the perpendicular bisector of CD since they are both equidistant from points C and D
Since F is a point on the extended line through X and O, it bisects CD
Therefore XF is perpendicular to CD

That makes CF = DF
And triangle OFD is a right triangle having right angle F

Now we have

{\overline{XF}}^2 + {\overline{DF}}^2 = {\overline{XD}}^2

and

{\overline{OF}}^2 + {\overline{DF}}^2 = {\overline{DO}}^2

or, rearranging...

{\overline{DF}}^2 = {\overline{DO}}^2 - {\overline{OF}}^2

but since XF = XO + OF, we have

(\overline{XO} + \overline{OF})^2 + {\overline{DF}}^2 = {\overline{XD}}^2

Substituting for DF, we get

(\overline{XO} + \overline{OF})^2 + {\overline{DO}}^2 - {\overline{OF}}^2 = {\overline{XD}}^2

{\overline{XO}}^2 + 2 \cdot \overline{XO} \cdot \overline{OF} + {\overline{OF}}^2 + {\overline{DO}}^2 - {\overline{OF}}^2 = {\overline{XD}}^2

{\overline{XO}}^2 + 2 \cdot \overline{XO} \cdot \overline{OF} + {\overline{DO}}^2 = {\overline{XD}}^2

2 \cdot \overline{XO} \cdot \overline{OF} = {\overline{XD}}^2 - {\overline{XO}}^2 - {\overline{DO}}^2


\overline{OF} = \frac{{\overline{XD}}^2 - {\overline{XO}}^2 - {\overline{DO}}^2}{2 \cdot \overline{XO}}

We know that XD = 8, XO = 5, and DO = 5 so, substituting we get


\overline{OF} = \frac{8^2 - 5^2 - 5^2}{2 \cdot 5} = \frac{64 - 25 - 25}{10} = \frac{14}{10} = 1.4

OF is the perpendicular distance from the center of the circles to line segment CD and it's length is, indeed 1.4cm