- #1
AdityaDev
- 527
- 33
In my textbook, its given that the equation of family of circles touching a given circle S and line L is ##S+\lambda L=0##
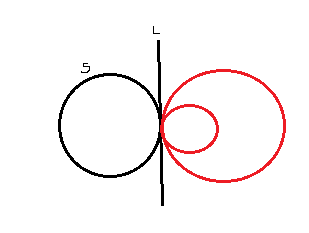
So to find the equation of family of circles touching line L at point P(p,q), can i use the same equation taking S to be a circle of radius zero and center at P?
That is, if L is ax+by+c=0 and P is (p,q), then S will be ##(x-p)^2+(y-q)^2=0## and the equation of family of circles will be ##(x-p)^2+(y-q)^2+\lambda (ax+by+c)=0##. Is this correct? such a circle passes through P.
So to find the equation of family of circles touching line L at point P(p,q), can i use the same equation taking S to be a circle of radius zero and center at P?
That is, if L is ax+by+c=0 and P is (p,q), then S will be ##(x-p)^2+(y-q)^2=0## and the equation of family of circles will be ##(x-p)^2+(y-q)^2+\lambda (ax+by+c)=0##. Is this correct? such a circle passes through P.